簡単に「かけ算」「わり算」で終わらせてはいけない。
３年生でも「倍の計算」として登場しますが、それの４年生バージョンです。
この単元は、「何倍に関する問題」が、以下の３パターン用意されています。
・何倍かを求める問題。
・比べられるものの値を求める問題。
・もとの値を求める問題。
なんとなくかけ算かわり算にあてはめると答えがでてくるので、指導がラクなように見えます。
ただ、この単元のねらいは、単純に問題を解くのではなく、問題の中に出てくる関係を整理することだと思います。
そうすることで、５年生や６年生で習う分数倍や小数倍、または割合、速さが理解しやすくなるのではと思います。
この単元で大切にしたことは、
・登場するものは２つで、それらが比べ合っていることを知る。
・その２つの関係を整理する。
・２つの関係を数直線で表す。
これらの手順で、倍の見方の単元を進めていきました。
何倍の問題は、２つを比べ合っている。
では、指導実践です。
先生「今日は、あるものとあるものを比べて、どちらがどれだけの量になるのかを考えながら答えを出していきます。」
先生「親のクジラがいます。」
黒板に親クジラをはります。
先生「子どものクジラがいます。」
続いて子クジラをはります。
先生「親のクジラの身長は、子どものクジラの身長の何倍？」
子ども「う〜ん。３倍くらい？」
先生「それくらいかな。今、３倍くらいって言ってくれたけど、何を基準（もと）に３倍って言ったの？」
子ども「子どものクジラ」
先生「そうだよね。この何倍かを求める問題は、基準となる相手がいないとわからないよね。今回は、親と子どものクジラ。何倍かを求める問題の中で登場するものは、２つしかありません。この２つを比べ合っていることになります。」
「比べ合う」という表現がいいのかわかりませんが、子どもたちには理解しやすいかと思い、使っていきました。
まず、「倍の見方」の単元でおさえたことは、登場するものは２つしかない。それを比べ合っているということです。
２つの関係を整理する。
先生「問題です。」
子どものクジラの体長は３mで、親のクジラの体長は１５mです。
親のクジラの体長は、子どものクジラの体長の何倍ですか。
子ども「簡単。５倍」
そう、簡単なのです。すぐに答えがわかります。
先生「正解！ただ、今日はこの親子のクジラの関係をくわしく整理していきます。」
この関係を知ることが、今後の割合や小数倍につながります。
先生「この問題に登場するものは何？」
子ども「親クジラと子クジラ」
先生「それぞれの体長はどれだけですか。」
子ども「親は１５m、子供は３m」
先生「この問題で知りたいことは何？」
子ども「親は子どもの何倍か。」
親クジラのところに、子どもの□倍と書きます。□倍だけではなく、「子どもの□倍」と書くことで、親か子のどちらに書くか迷わずにすみます。
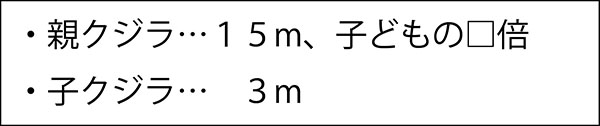
先生「そうだね。子どもを基準（もと）にして、親はどれだけの体長かを知りたいんだよね。こどものいくつ分かを知りたいから、子どもは１（１倍）とします。」
先生「基準（もと）は、必ず１（１倍）です。」
２つの関係を数直線で表す。
次はこの関係を数直線で表します。
５年生以上で出てくる数直線を先取りします。
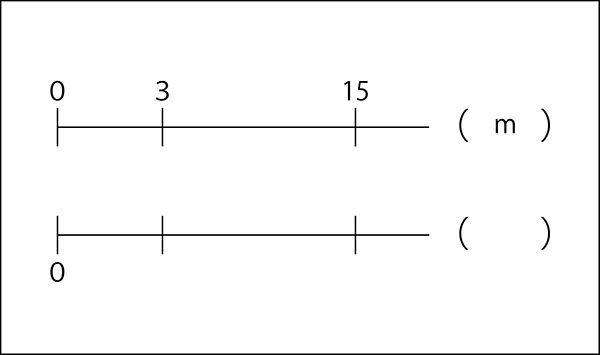
先生「数直線に、親と子のクジラの関係を書いていきます。」
先生「それぞれの体長を書きます。」
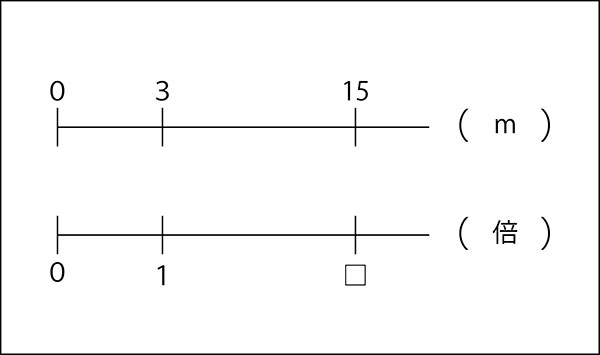
先生「それらが何倍かを下に書きます。」
文章題からでは、なかなか数直線に書き出すことは難しいです。
関係を整理したことで、数直線に書きやすくなりました。
この関係から１５÷３をひも解くわけですが、私はもとの１から考えさせます。
先生「１の□倍が□なので…」
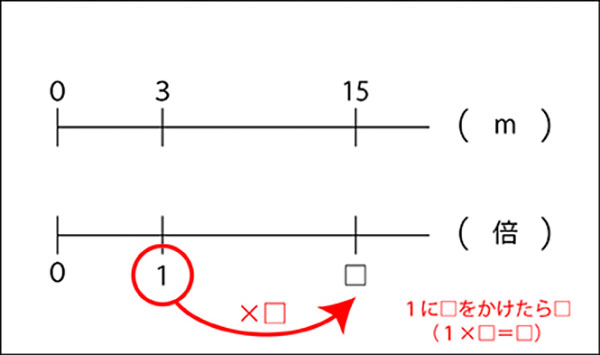
先生「３mの□倍が１５mということがわかるね。」
３×□＝１５と黒板に書きます。
先生「３×□＝１５から、□はどのように求めますか。」
子ども「１５÷３」
先生「ただの１５÷３でも、こんな関係があるんだね。」
このあと、ワークシートで練習問題をして終了しました。
↓練習問題のワークシートはこちら↓
くじらの掲示物もついてますよ！
実践してみて
「この関係を整理することが、５・６年でも大切だよ。」
と言っても、中には「さっさと１５÷３したらいいじゃん」と思っている子もいると思います。
また、５年になって担当の先生が変わると、指導の仕方も変わるでしょう。
ただ、関係を整理して数直線に当てはめることができるようになると、わざわざ割合の「くもわ」や、速さの「みはじ」などに頼る指導をしなくてよくなると思います。
５・６年につながる、とても重要な単元だと思いました。
ご意見いただけら幸いです。
↓その２に続く！↓
４年算数「倍の見方」指導実践その２ 比べられる量を求める
５年算数 数直線で単位量の理解が深まる！「単位量 導入の前に確認すること」指導実践
