Keynoteを使って考えました。
ひし形の面積の求め方も台形のときと同様、ヒントとなる動画を見せて、そこから公式まで導くことにしました。
ただ、教科書には、「〇〇さんの求め方を説明しなさい。」と書かれているので、見て説明させることも大切なのかなと思います。
なので、今回は説明に意識をおいて授業に取り組みました。
では、指導実践です。
先生「↓今日は、こんな形の面積を求めます。どんな形?
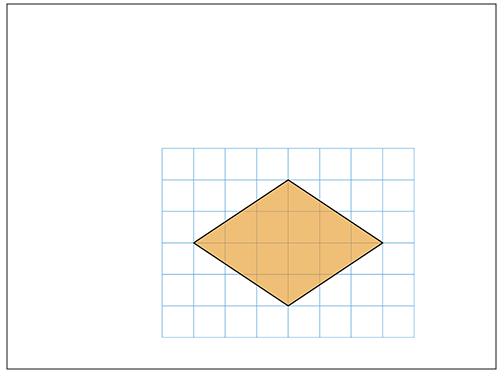
子ども「ひし形!」
ひし形について簡単に特徴を振り返ります。
そして、いつもの複雑な図形の求め方について簡単に振り返ります。
- 切り分けたり、付けかえたり、付け足したり、引いたりして、簡単な図形に形を変える。
- もとの図形の情報を使って求められるか考える。
- 公式にする。
先生「↓ひし形は、こんな簡単な図形に変えて求めていきます。」
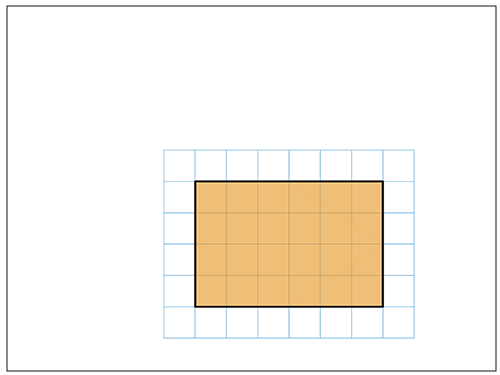
子ども「長方形だ。」
先生「↓もとの形はこう。赤い部分が追加されたところだね。」
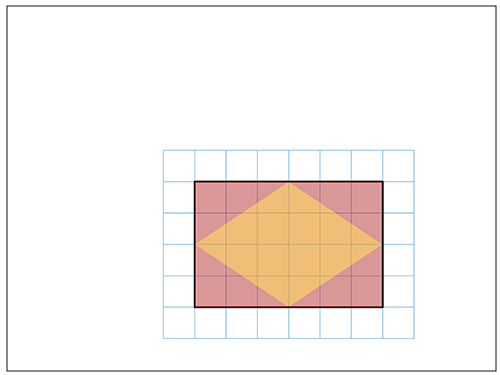
この時点で気づいた子もいるようです。近くの子と話が始まりました。
先生「↓赤い部分を合わせると…。」
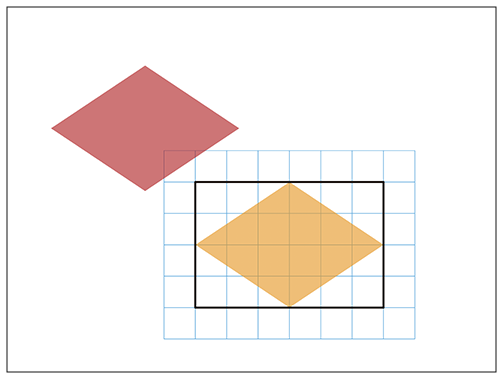
先生「↓そして、もとの形と重ねてみます。」
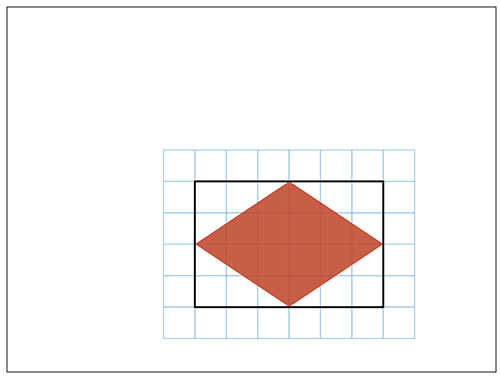
先生「どうなった?」
子ども「同じ大きさ!」
先生「ここまでみて、ひし形はどういう風に求められるか考えてみましょう。」
ペアトークをさせます。
子ども「ひし形を長方形の形に変えて、あまったところがひし形と同じ大きさだから、長方形を半分の大きさにすれば求められる。」
スライドをもう一度見せて確認します。
もとの形から求められるか考えていく。
先生「↓じゃぁ、もとの形から求められるか考えていこう。どの部分が使える?」
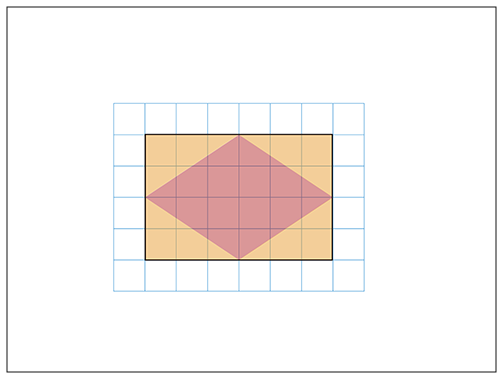
子ども「長方形のたてと横の長さ。」
先生「↓なるほど、この赤の部分だね。そしてその後…。」

子ども「÷2をすればいい。」
先生「↓でも、こんな風に実際にひし形を求める時、長方形なんかかいてるかな?方眼もない時あるけど、どうしようか?」

先生「この長方形のたてと横の長さは、このひし形のどの部分と同じといえるかな?」
子ども「対角線!」
先生「↓その通り!長方形のたてと横は、対角線で補えそうだね。」
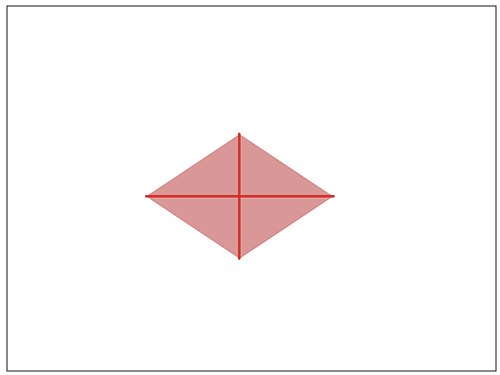
これで、公式「対角線×対角線÷2」ができました。
この後、これまでの流れを自分で振り返り、説明し合いました。
授業を振り返って
時間がない中での授業となりました。
本当なら、子どもたちに自力で求め方を導き出させるのがいいのかもしれません。
ご意見頂けたら幸いです。
今日の資料はここ!
今回の記事で紹介したスライドもあります。もし、よければご活用ください。
感想もお待ちしております。