第5時は、自分たちで問題を作りながら、わり算には等分除と包含除のちがいがあるということをより理解する時間とします。
では実践報告です
先生「今日は自分たちで問題を作ってもらいます。」
先生「6このあめを分けます。6÷2になるように問題を作ってごらん。」
ふたつの問題ができます。
どちらかひとつの問題が書けたらオッケーです。
書けたら発表してもらいます。
- 6このあめを2人で同じ数ずつ分けると、1人分は何こになりますか。
- 6このあめを、1人に2こずつ分けると、何人に分けられますか。
先生「自分が書いた問題の図がかけますか?」
ノートに図を描いてもらい、あとで発表してもらいます。
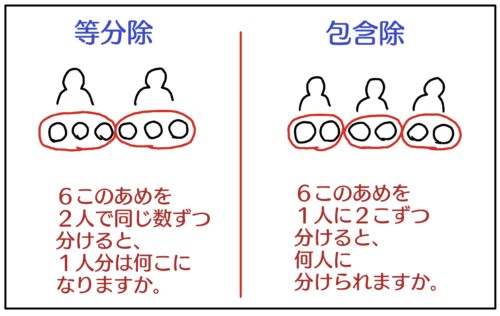
等分除と包含除では、式は同じでも図で表すと意味が変わるのが一目瞭然です。
まとめ
先生「まとめだけど、今日はみんなに考えてもらいます。」
理想は
1人分の数をもとめる時も、何人に分けられるかをもとめる時も、わり算でもとめられるが、分け方や意味がかわってくる。
ですが、難しいので赤い字のところを穴埋めにしました。
あとは練習問題です。
このあと12÷3や24÷4など、それぞれの式になるように問題をつくらせ、そのたびに図を描かせて確認させます。
問題を多く解かせることで、わり算の2つの意味に気づいてくれればと思います。
ご意見頂けたら幸いです。
https://kuronekoneko.com/3nenwarizan6/


