整数÷小数
いよいよ小数でわる計算の仕方を指導します。
とは言っても、4年生までやってきたことをふまえて指導すれば、そんなに難しくないのではと思っています。
そして、前回のブログでも書いた記事の内容も、今回の授業に生かすことができればと思っています。
 5年算数「小数のわり算」指導実践1「導入前に教えること」
5年算数「小数のわり算」指導実践1「導入前に教えること」 では実践報告です。
先生「さて、今日から5年生の小数のわり算の勉強です。4年生の時とどこが違うのか、比べながら進めてほしいと思います。」
問題を書きます。
リボンを2.5m買ったら、代金は300円でした。
このリボン1mのねだんは何円ですか。
先生「これは何算?」
子ども「わり算です。」
先生「Aタイプ?Bタイプ?」
前回、わり算は2つの意味(AタイプとBタイプ)があると指導しました。
詳しくは前回の記事で紹介しています。
子ども「Bタイプです。」
先生「何で?」
子ども「1mあたりを求めるからです。」
先生「そうですね。1あたりを求めるのはわり算でしたね。2.5mの1m分の値段を求めます。式は?」
子ども「300÷2.5です。」
先生「4年生の時の小数のわり算と違うところはどこかな?」
子ども「わる数が小数になっているところです。」
先生「そうだね。」
これはおさえないといけません。
先生「2.5mの1m分の値段…。一体どれくらいだろうね?」
数直線で見てみます。
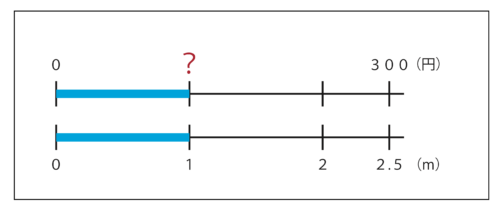
先生「2.5mの1m分って、何か中途半端な長さだね。」
今まで整数でしかわったことがないので、不思議な感覚だと思います。
先生「でも、こんな中途半端な長さを求める時も、1あたりを出すのはわり算なんだよね。」
ゴリ押し感がありますが…。
先生「この図で見ると、だいだいどれくらいの値段かなぁ。」
検討をつけさせます。
子ども「うーん、100円ちょっとかなぁ。」
先生「じゃあ、本当に100円ちょっとになるか、授業を進めていこう。」
わり算の性質を思い出させる。
先生「式は300÷2.5でした。はじめて小数でわります。わる数が小数じゃなくて、どんな数字だったらわりやすい?」
子ども「整数。」
先生「そうだね。整数なら、今まで通りわれる。じゃあ、計算しやすいように形を整数に変えてあげよう。」
スライドを見せます。

先生「4年生の時、こんなわり算の性質を習いました。この性質を使って問題を解くんだけど、わかるかな?」
ヒントは、72÷8=9 7200÷800=9 です。
子どもに答えさせます。

先生「この性質を使えば、300÷2.5も解けそうだね。お互い何倍すれば整数になる?」
子ども「それぞれの数を10倍してあげて、3000÷25にしてあげる。」
先生「じゃあ、計算してみようか。」
3000÷25は既習事項ですが、忘れている子もいるので、丁寧に計算していきます。
子ども「答えは120円だ。」
先生「予想した通り、100円ちょっとだったね。」
子ども「本当だ。」
先生「小数でわる場合も、1あたりを出すことができたね。今日は、小数でわる計算の仕方を勉強しました。まとめます。」
まとめ
小数でわる場合は、わる数を整数に形をかえると、答えが求めやすくなる。
この後、類似問題をします。
まだ、小数の筆算は行いません。
それぞれの数を10倍して計算することを徹底して終了しました。
感想
とにかくわり算は1あたりを求めるということをゴリ押しして進めた授業となりました。
なんでそうなるんだろうと、疑問に思う子もいたかと思います。
また、教科書には0.1を基準にして考える方法ものっていました。こちらの方法だと、納得する子も多くいたでしょう。
ただ、両方扱うとこんがらがると思ったので省略しましたが、確認として教師が提示してあげてもよかったかもしれません。
何よりお互い10倍するやり方の方が、今後の小数の筆算の考えに直結します。
そして、授業時間とのやりくり…。
やっぱり難しい単元だなぁ…!
ご意見頂けたら幸いです。

