約数の法則を見つける
約数の第2時です。
前回は、数字がバラバでもいいので約数を書き出すことまでを行いました。
人間は忘れる生き物です。
もう約数を忘れている子もいます。
本題に入る前に、もう一度同じ問題でもいいので練習問題を取り入れました。
そして、その中から18の約数を取り上げ、
先生「数を小さい方から順番にならべてごらん。」
と、指示を出します。

先生「この数字を見て、何か気づくことない?」
子ども「なーい」
なんて、声もきこえましたが…。
外側同士の数字をかけていくと、もとの「18」の数字になることに気づいてほしいのですが、なかなか答えてくれませんでした。
なので、
先生「1と18をかけると…」
子ども「18」
先生「なるほどね〜」
なんていうさりげないヒントを出していくと、気づいた子もちらほら出てきました。
子ども「1と18をかけると18、2と9をかけると18、3と6をかけると18!」
線でつないでいきます。
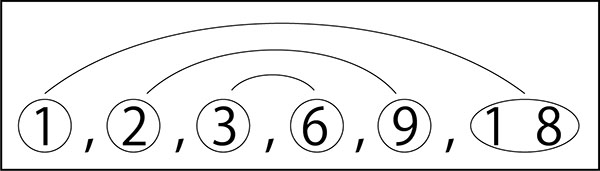
虹のようになるので、「レインボーの法則」と名づけました。
先生「約数を見つけるときに役立ちそうだね。」
レインボーの法則を使って、約数を見つける練習をする。
先生「じゃあ、12で確認してみよう。」
これまでも出てきた数字ですが、その方がいいかもしれません。
先生「必ずある数字なんだっけ?」
子ども「1」
第1時で確認していました。
先生「レインボーの法則だと、1と何をかけようか」
子ども「12」

少しきょりを置いて書かせます。
先生「1の次は何がありそう?」
子ども「2」
先生「ということは…」
子ども「6!」

先生「2の次は?」
子ども「3!」
子ども「4とかけて12」
先生「もうある?」
子ども「ない」
レインボーにします。

レインボーの法則のよさを見つける
約数の多い24を扱ってみます。

先生「この法則で約数を見つけるよさはありますか?」
子ども「ペアがある」
子ども「外側から見つけるから、残りの約数が限られてくる」←(こんな的確なコメントではありませんでしたが)
16の約数を扱う
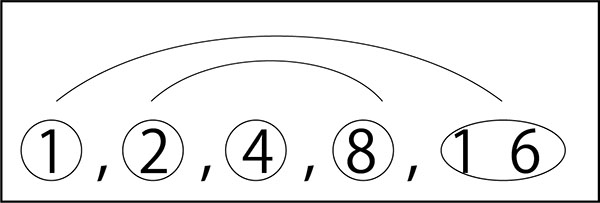
子ども「あれ?4はどうしたらいい?」
先生「4に何をかけたら16?」
子ども「4」
先生「ペアがない場合は、その数字は2つあるってことなんだね。」
練習問題をレインボーの法則で行なっていく
このあと、「25」「15」「9」「19」などの数字を扱って行きます。
「36」や「48」はやりがいがあるので、上級レベルとして出してみました。
先生「必ずしもこの法則で見つけなければいけないことはないけれど、書きもれがないか確認できるね。」
と言って終了しました。
ご意見頂けたら幸いです。