組み合わせ方を考える時、いくつかの考え方が教科書に載っています。
問題解決で、子どもたちに探させるには出てこない考え方もあります。
全てを子どもたちに委ねるのではなく、こちらからいくつかやり方を提示して進めていく方向で指導を組み立ててみました。
では指導実践です。
先生「バスケットの試合をA、B、C、Dのチームで全部のチームと1回ずつ対戦します。Aはどのチームと対戦する?」
子ども「B、C、D」
先生「Bチームは?」
子ども「A、C、D」
という具合に書き出してみます。

先生「じゃあ、試合の数は12通りだね。」
子ども「なるほど。」
と、このまま終わりそうだったので…
先生「何か気づかない?」
子ども「??」
先生「今回は対戦だよね。A対Bと同じものを表す対戦ないかな?」
子ども「あ、B対A。」

先生「そうだよね。順番がかわろうが意味は変わらないよね。」
ということで、同じ意味のものを消していきました。

全部で6通りになりました。
いろいろな求め方を紹介する
今回の組み合わせ方を求めるとき、教科書にあるような求め方を子どもたちに期待するのは、難しいと思います。
こちらから紹介して、どういう意味なのかを考えていくことにしました。
対戦表
先生「これも組み合わせを表しているよ↓」
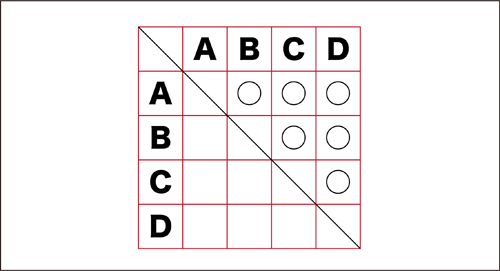
対戦表になじみのない子が多く、説明からはいらないといけませんでした。
先生「ここと同じ意味を持つところはがあるよ。」
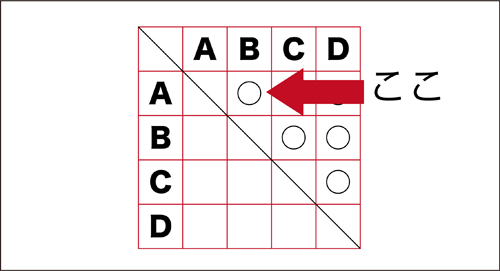
子ども「ここ↓」
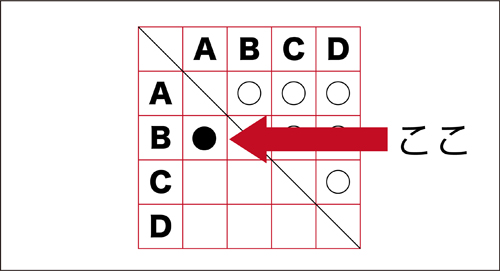
先生「そうそう、だから、同じところはかいてないんだね。」
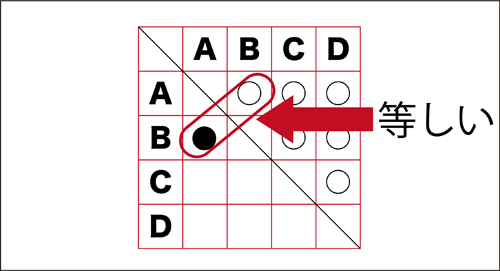
先生「まるは、どこに集まっている?」
子ども「線の上半分。」
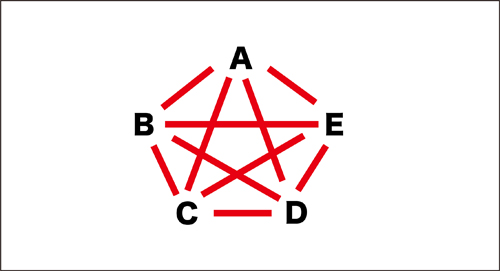
辺と対角線の数
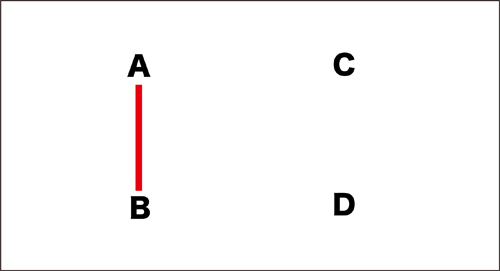
先生「こんな考えもあるよ↓」

先生「AとBが対戦するとき、こうしてつなぎます↓」
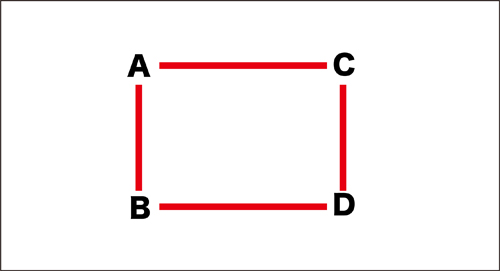
そして、子どもたちに聞きながらその他の線もつないでいきます。
先生「もうないかな?」
対角線にはなかなか気づきませんでしたが、最後まで線を引きます。
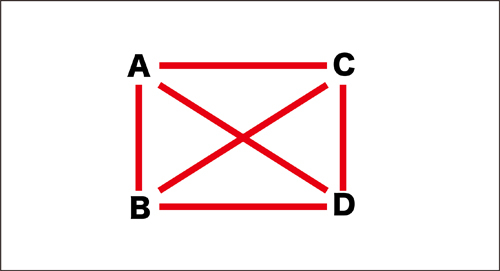
先生「この線の数が対戦の数になるね。」
実際、この考えが一番簡単です。
この後、5つの中から組み合わせを考えるとき、対戦表で考える子が多かったですが、この考えで求めていくと、「な〜んだ、簡単」と、よろこんで星形をかいていました。
ご意見頂けたら幸いです。