今回の問題です。
〈問題〉
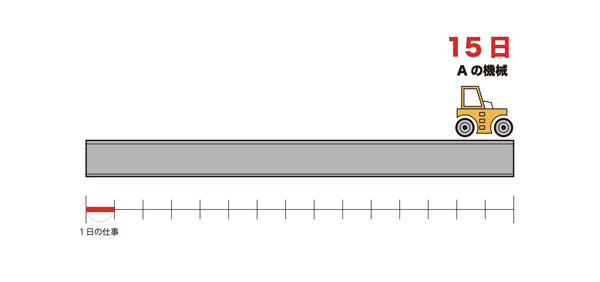
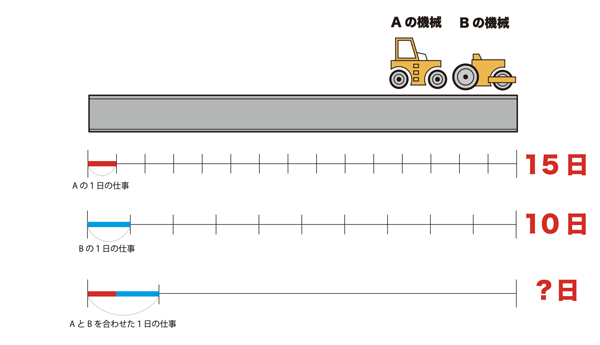
ある道路をほそうするのに、Aの機械では、１５日、Bの機械では１０日かかります。
A、Bの機械を同時に使うと、この道路をほそうするのに何日かかりますか。
公倍数で求める
全体を公倍数で求める場合と、全体を１とみて求める場合がありますが、全体を公倍数で求める場合で指導しました。
今回はパワーポイントのapple版「keynote」を交えながら指導しました。
今回作ったkeynoteのスライドを、試験的にgoogle driveを使って共有いたします。
よければどうぞ！keynoteの資料はこちら。
では指導実践です。
先生「道路を舗装します。Aの機械だと…。」
先生「舗装するのに１５日かかります。」
先生「１日にどれだけ舗装するんかなぁ。」
子ども「そんなのわかんないよ。」
先生「なんで？」
子ども「だって長さがわかんないじゃん！」
先生「そうなんだよね〜。長さがわかんないんだよね。でも、今日は全体の長さを勝手に決めていいことにします。」
子ども「え？いいの？」
先生「今日の勉強のポイントです。今日は、全体を勝手に決めて求める勉強をします。」
子ども「おお〜。」
先生「ちなみに、勝手に決めるとすると、何mがいい？」
子ども「１５mとか３０mとか。」
先生「何で？」
子ども「わり切れるから。」
先生「そうだね。わかりやすい方がいいよね。」
そして、道路を数直線に置きかえると、１日分がどれくらいの長さか確認しました。
同じように、Bの機械も確認します。
先生「今度は、２台同時に舗装しました。２台で１日に舗装できる長さって、どれくらいの長さになる？」
子ども「AとBをたしたやつ！」
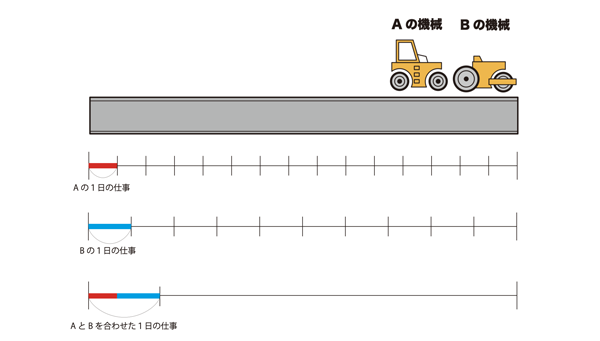
先生「そうだね、合わせるといいよね。Aだけだと１５日、Bだけだと１０日、じゃぁ合わせると何日で仕事が終わるだろうね。」
と、ここで黒板に問題を書きました。
〈問題〉
ある道路をほそうするのに、Aの機械では、１５日、Bの機械では１０日かかります。
A、Bの機械を同時に使うと、この道路をほそうするのに何日かかりますか。
先生「これが、今日の本題です。今回のポイントはなんだったっけ？」
子ども「勝手に決める！」
先生「そうだったね！でも、Aの時もBの時も道路の長さはちがってもいい？」
子ども「だめ！」
先生「勝手に決めたいんだけど、どんな数字がいいって言ってたっけ？」
子ども「わかりやすい数。」
先生「勝手に決めていいけど、Aの時もBの時も共通してわかりやすい数字にしないといけないね。」
子ども「３０mがいい。」
先生「３０mだとどうなるの？」
子ども「３０mだと、Aは１日２mって出て、Bは1日３mって出るからわかりやすいから。」
先生「なるほど！３０っていう数字は１５と１０の何だったか覚えてる？」
子ども「最小公倍数！」
先生「そうだね。公倍数を求めると、それぞれの数字でわれることができるよね！じゃぁ、AとBを合わせると１日何m舗装できる？」
子ども「５m！」
先生「じゃぁ、何日かかるかもうわかるね！」
あとは、３０m÷５mをするだけです。
先生「勝手に決めた数が他の数ならどうなるだろうね。」
といって、６０の時や９０の時も計算して確かめてみました。どれも６日なることを確認しました。
ご意見頂けたら幸いです。
６年算数「組み合わせ方」指導実践 具体例を挙げ、子どもたちと考えていく
６年算数「比 導入」指導実践 ソースとケチャップで進めていく。
６年算数「角柱と円柱の体積 導入」指導実践（資料付き）
６年算数「比例」指導の時に使える素材集です！授業準備にどうぞ！
