3年生の重要単元「わり算」
「わり算」という言葉を知らない子は少ないと思いますが、やってみると意外に「??」な子も多く、ていねいに扱いたい単元です。
初めて「分ける」という概念です。
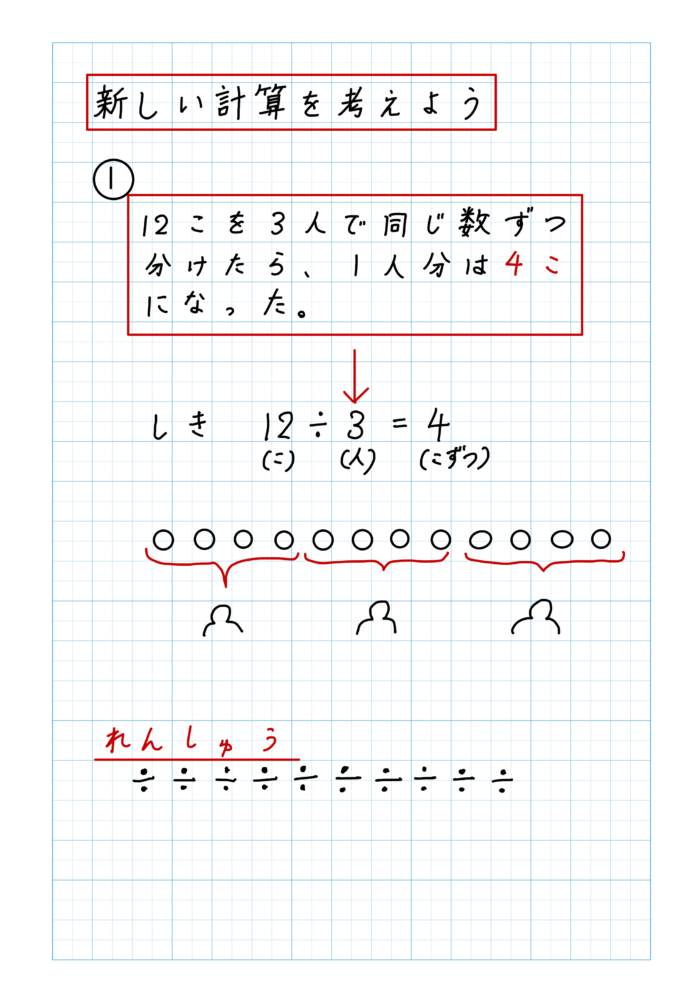
第一時では、「12このクッキーを3人で同じ数ずつ分けると、1人4個ずつになった。」を、「12÷3=4」という式で表すことができるということをめあてに授業を組み立てました。
では実践報告です。
「分ける」の勉強
先生「今日は、『分ける』ということを勉強します。」
教科書の問題は、
「12このクッキーを3人で同じ数ずつ分けます。1人何個ずつになりますか。」
でした。
しかし、この問題を提示すると、塾に行っている子や勘のいい子はすぐに「4個」と答えを出すので、

といった具合に、袋の中に何個あるかわからないようにし、
先生「どうすれば、同じ数ずつ分けることができるかな。」
と問います。すると、
子ども「1個ずつ渡していけばいいと思う。」
と答えてくれました。
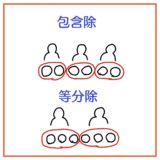
教科書通り、等分除での分け方に自然となります。
先生「では、1個ずつ渡していきます。」
といって、「ひとーつ、ふたーつ…。」と数えながら実際に3人の子どもたちに渡していきます。
もちろん、袋には12個のクッキーが入っています。(ニセモノですが…)

12個を渡し終えたあと、
先生「今、何このクッキーを何人で同じ数ずつ分けたら、1人何個ずつになりましたか?」
子ども「12個のクッキーを3人で分けたら、1人4個ずつになった。」
この言葉が、この授業でとても重要です。暗記してもいいくらいです。

先生「今の言葉を式に表すと、こうなります。」
といって、12÷3=4を紹介します。

先生「この計算をわり算といいます。」
言葉を式に置きかえました。
そして、「÷」の書き方も練習します。
さらには図もかいて、12個を3人で分けると4個ずつになるということを確認します。
類似問題で定着する。
次は、袋に8個のクッキーを入れ、2人の子どもで分けます。もちろん、袋に何個クッキーが入っているかは子どもたちには伝えません。
そして、先ほどと同じように
先生「今、何このクッキーを何人で同じ数ずつ分けたら、1人何個ずつになりましたか?」
と問います。
子ども「8個のクッキーを2人で分けたら、1人4個ずつになった。」
先生「この言葉を式に置きかえなさい。」
といって、「8÷2=4」と書きます。
先生「今日は分けた時、どんな式になるか勉強しました。12÷3=4や8÷2=4のような分ける計算は何と言いましたか。」
子ども「わり算です。」
といって、最後はノートにまとめます。
やってみて感想
わり算という新しい概念ですので、子どもたちをレールに乗せ、教え込んだ感はありますが、基本を教えるのは大切だと考えています。
これでもまだ、「わり算の意味がわからない」と答えた子は、2人ほどいました。
ノートにはこう書きました。
よければ参考に。

ご意見頂けたら幸いです。
↓続きはこちらから!↓