Keynoteを使って考えました。
台形の面積では、ヒントとなる動画を見せて、そこから公式まで導くことにしました。
なかなか授業時間が取れない中だったので、シンプルに授業ができないかを考えて実践しました。
動画を見ることで、平行四辺形の半分ということがわかります。
では、指導実践です。
まずは、これまで平行四辺形や三角形の面積を求めてきた時の流れを確認します。
- 切り分けたり、付けかえたり、付け足したり、引いたりして、簡単な図形に形を変える。
- もとの図形の情報を使って求められるか考える。
- 公式にする。
台形の特徴を簡単におさらいした後、求め方の動画を見せました。
先生「まずは、複雑な面積を求める時、簡単な図形に変えて考えるんだったね。どんな図形に変わった?」
子ども「平行四辺形!」
先生「どうすれば、平行四辺形になったかな?」
子ども「台形を2つ合わせた。」
先生「じゃぁ、台形を求める時、平行四辺形に形を変えた後、どうすればいい?」
子ども「半分にする!」
先生「そうだね!まずは平行四辺形を求めよう。平行四辺形に変えた時、もとの台形の情報を使って求められるか確かめてみよう。」
下の資料を子どもたちに配布します。
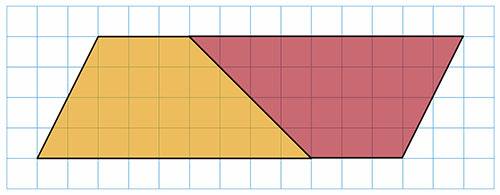
先生「底辺の長さは?」
子ども「12cm。」
先生「これって、台形のどの部分の長さのことになる?」
子ども「上の辺と下の辺をたした長さ。」
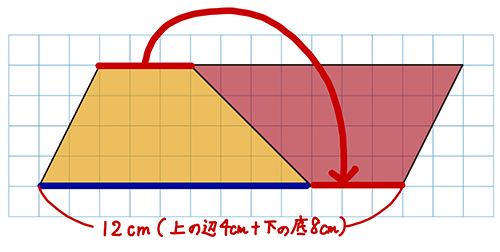
先生「高さは?」
子ども「4cm。台形の高さがそのまま使える。」

先生「そしたら、平行四辺形の面積は?」
子ども「12×4で48㎠」
先生「じゃぁ、台形の面積は?」
子ども「半分なので、24㎠」
先生「確認します。台形の面積は、何に形を変えてからどうしますか?」
子ども「平行四辺形に形を変えてから半分にする。」
この後、公式にしました。
練習する時間を確保する。
シンプルに授業を進めることで、1時間で練習時間できました。
多様な意見を出し合うことも大事ですが、ここではなぜ台形の面積を求める公式が(上底+下底)×高さ÷2なのかを理解することを大事にしました。
ただ、授業をしても忘れるのが人間です。
繰り返し復習する機会を与えることが最も重要だと思います。
今日の資料はこちらです。
今日の資料はここ!
動画はkeynoteで作成しています。あと、授業で使った掲示用の台形の図形や、子どもたちに配布した資料もあるのでよかったらどうぞ!
ご意見頂けたら幸いです。