シンプルに
5年生の学習を振り返ると…
・小数の倍
・単位量
・速さ
これらの単元は、かけ算・わり算を使う単元になります。
割合に進むにあたり、これらの単元全て図を用いて、問題を解いてきました。
はじめは教科書のような数直線を使っていましたが、4マス関係図で簡略化していきます。
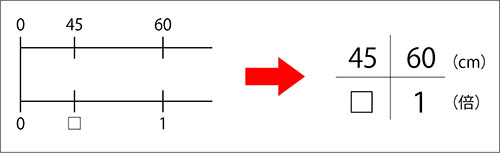
「1あたりはどれだけか」「1あたりのいくつ分はどれだけか」「1あたりの何倍か」など、
図を用いることで「見える化」し、理解を深めてきました。
小数の倍、単位量、速さと、それぞれの単元で扱っているものがちがうだけで、結局はかけ算とわり算。やることは一緒です。
そして、今回の割合もかけ算とわり算が出てきます。
これまで通り、図を用いて学習を進めてきたので、割合もスムーズに授業を進めることができました。
では、指導実践です。
これまでの復習から入り、それが割合になっていることを確認していきました。
問題1
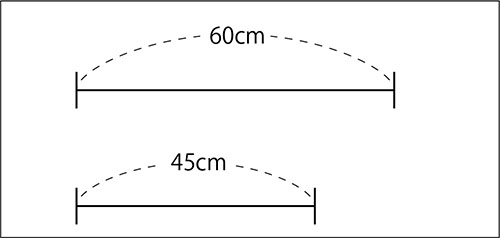
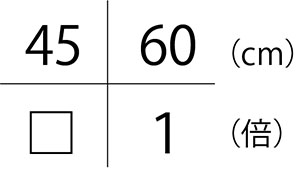
Aの60cmを1とみると、Bの45cmは何にあたりますか。
今までに出てきた問題です。
4マス関係図を用いて解いていきます。
式
45÷60=0.75
答え
0.75
続いて問題を解きます。
問題2
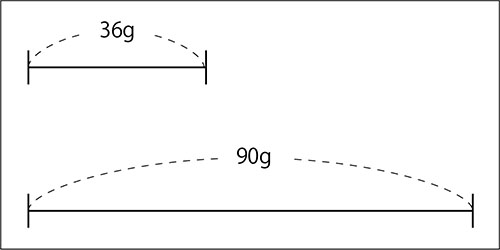
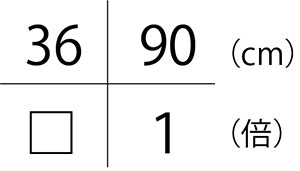
Aの36gはBの90gの何倍ですか。
これも図を用いて解いていきます。
式
36÷90=0.4
答え
0.4
あと数問出しました。
先生「さて、今日から割合という単元に入りますが、もうすでにこれが割合です。」
子ども「えー!今までやってきたじゃん。」
先生「問題1は、1に対して0.75にあたったね。この1を100%として考えます。すると、0.75は…。」
子ども「75%!」
ノートにもつけ足していきます。

先生「そうそう!パーセントで言った方がイメージしやすいでしょ?」
軽く百分率にも触れていきます。
先生「問題2も90gがもとだったよね。90gを100%として考えると、36gは…」
子ども「40%!」
先生「もとに対して比べられた量がどれだけにあたるかを割合と言います。次回からこの割合をより詳しく見ていきます。」
これで導入が終了しました。
教科書には必ず図が
3年生くらいからこの数直線の関係が教科書にも載っています。
3年生のかけ算やわり算は、文章からなんとなく式をたてることができますが、5年生になると、小数や分数などで計算するので、そうはいきません。
3年生からしっかりとこの数直線をていねいに触れることで、割合をはじめ、速さや単位量もよりスムーズに進むはずです。
毎年先生が変わり、教え方もさまざまになるので、学校全体で指導の仕方を確認することが大切なだと思いました。
ご意見頂けたら幸いです。