研究授業で行った実践です。
大学の先生にもアドバイス頂き、発問を精選することで、めあてに向かって活動させることを目標としました。
では実践報告です。
まずは導入
先生「四角形があります。いくつの棒でできていますか。」
子ども「４本。」
先生「２つの場合は？」
子ども「８本。」
先生「じゃあ、四角形３この場合は？」
子ども「１２本。」
以下、四角形６この場合までリズムよく聞いていきます。
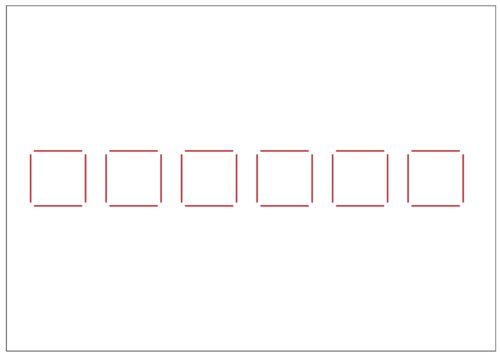
先生「四角形が１つふえるたびに棒の数は何本ずつふえる？」
子ども「４本ずつ。」
先生「増えていく数がきまっているから、全体の棒の数が求めやすいね。四角形が６この時、式はどうなる？」
子ども「４×６＝２４」
いよいよ今日の課題
先生「では、今度はこのようにつなげます。四角形が何こ見える？」
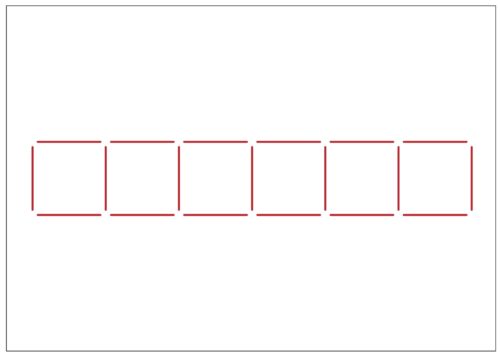
子ども「6こ。」
先生「棒を数えて。」
実際に指で数えさせます。ここでは答えは聞きません。
先生「せっかくの算数なので、今日は、６こにつないだ四角形の棒の数を、きまりを見つけて求めていきます。」
さきほどの導入の作業で、子どもたちに「きまり」のイメージがちょっとできたのではと思います。
ノートに、「きまりを見つけて」と書きます。
先生「四角形ひとつだっら棒の数は〜？」
子ども「４本！」
先生「２つなら？」
子ども「７本。」
先生「３つなら？」
子ども「10本。」
先生「4つなら？」
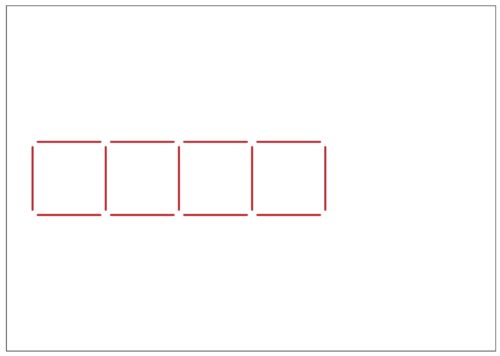
子ども「13本。」
先生「四角形がひとつ増えるたびに、棒は何本ずつ増えてる？」
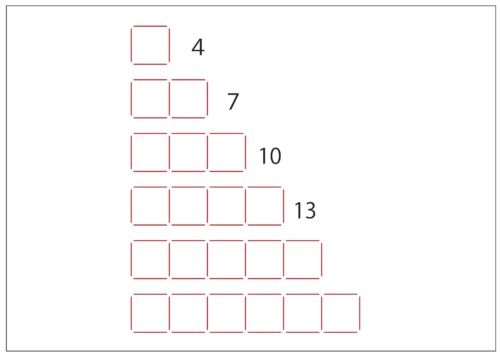
子ども「3本ずつ増えてる。」
先生「そっか。じゃあ、四角形が６こだと３×６で１８本かな。」
子ども「違うー！」
先生「え？でも、３こずつ増えてるんだよね。」
スライドと同じ６こつながった四角形の図を、子どもたちに渡します。
先生「なぜ３×６がダメなのか、考えを書いて。」
３こずつ増えていくことを強調し、なぜ３×６がダメなのかと問いかけることで、課題を焦点化しました。
なので、子どもたちが書いた考えにも、
「はじめの１本を足さないといけない。」
「はじめの四角形は４本だけど、２つ目からは、３本ずつ出せば四角形ができる。」
と、「３」というきまりの中でノートに考えを書くことができました。
この後、考えをもとにペアトークをし、発表させました。
長くなったので、後半に続く！
５年算数「変わり方を調べよう（２）」指導実践報告 後編