2つの量の関係を、3つのステップでおさえながら進めていく。
整数なら何となく求められるものが、小数になると、とたんにわり算なのかかけ算なのか分からなくなります。
そうならないように、問題に出てくる2つの関係を以下の3つのステップでおさえながら進めていきます。
・登場するものは2つで、それらが比べ合っていることを知る。
・その2つの関係を整理する。
・2つの関係を数直線で表す。
関係を整理することで、数直線にも表しやすく、式も立てやすい。
これができれば、今後の単位量や割合にも応用できると思います。
では指導実践です。
問題です。
10mの青のリボンは、4mの赤のリボンの何倍ですか。
まずは、問題に何が出てくるのか、そして、その2つの量の関係を整理していきます。
先生「何が出てきますか。」
子ども「↓青のリボンと赤のリボン。」

何倍の問題は、2つの量を比べることを理解させます。
先生「それぞれのリボンは何mですか。」
子ども「↓青は10m、赤いは4m。」
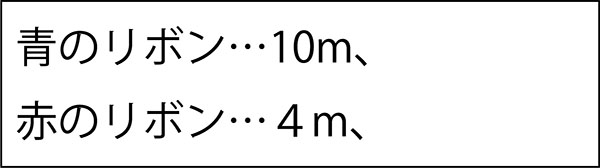
先生「青のリボンは、赤のリボンの何倍?」
子ども「わからない。」
先生「その場合は…」
子ども「□倍」
↓整理するときは、□倍だけではなく、赤の□倍と書きます。
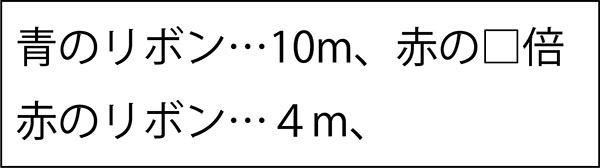
そうすることで、青と赤のどちらに書けばよいか分かりやすくなります。
↓先生「じゃあ、青は赤を基準(もと)にして何倍か知りたいんだよね。なので、基準の赤は1倍とします。」
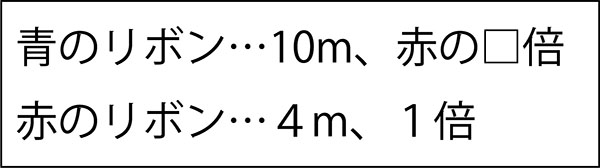
半ば強引ですが、基準となるもとの値は、1倍ということを植え付けていきます。
これで関係が整理できました。
2つの関係を数直線で表す。
↓関係が整理できたら、それをもとに数直線に表していきます。

↓まずは、長さ。その上にどちらのリボンの長さなのか書いておくと、よりていねいです。
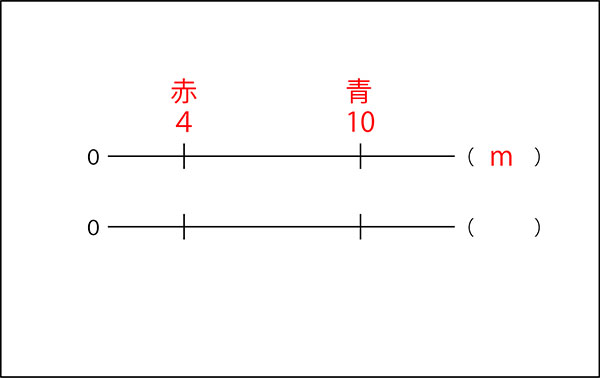
↓そうすると、その下の何倍かを書くときの間違いが少なくなると思います。
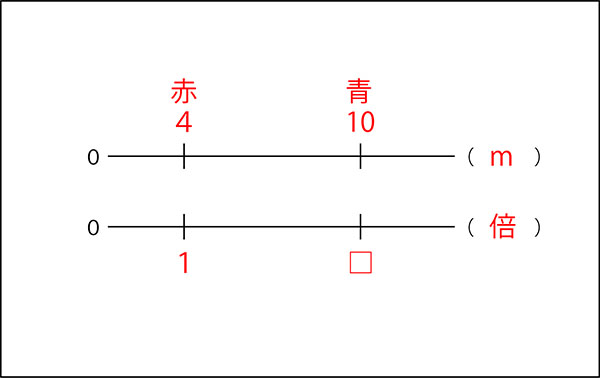
ここから式に導いていきます。
↓常に1の何倍から考えると、これからの問題にも対応しやすくなると思います。
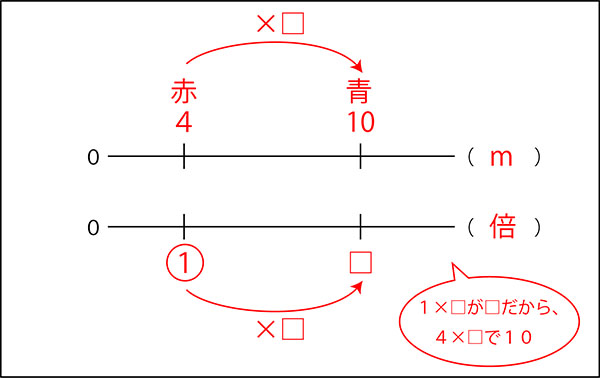
1×□=□だから、
4×□=10
10÷4=2.5
答えは2.5倍です。
青のリボンをもとにして考える。
次に、青のリボンをもとに赤のリボンが何倍かを考えます。
でも、やることはほぼ同じです。
問題です。
4mの赤のリボンは、10mの青のリボンの何倍ですか。
もう、この時点で多くの子どもたちは混乱するかもしれません。
でも、これまでと同様に2つの量の関係を整理しながら進めていきます。
先生「それぞれのリボンは何mですか。」
子ども「↓青のリボンと赤のリボン。」

先生「それぞれのリボンは何mですか。」
子ども「↓青は10m、赤いは4m。」
先生「赤のリボンは、青のリボンの何倍?」
子ども「□倍」
↓整理するときは、□倍だけではなく、青の□倍と書きます。
先生「じゃあ、今回の基準は…。」
子ども「青!」
↓青に1倍と書きます。
では、数直線に表していきます。
↓まずは、それぞれの長さを書きます。
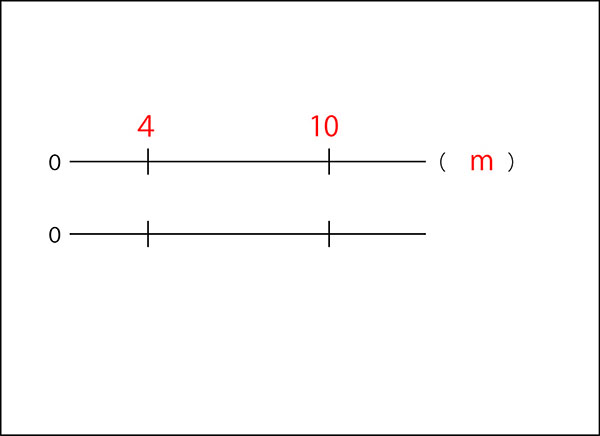
↓そして、それぞれが何倍かを書きます。
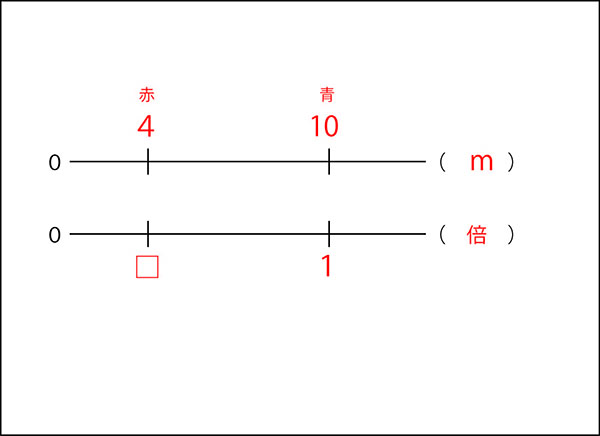
1より小さい割合が出てきます。
これが混乱する原因です。
でも、進めていきます。
先生「青より短いんだから、1倍より小さくなるのは当たり前だよね。」
実際に計算していきます。
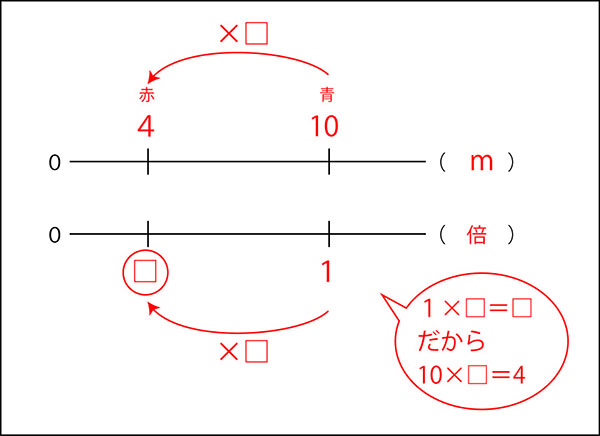
1×□=□だから、
10×□=4
4÷10=0.4
答えは0.4倍です。
あとは、教科書のまとめにもあるように、もとにする大きさをどちらかにするかで、倍を表す数が変わることをおさえます。
このように、小数の倍になるともとになる量が比べられる量より大きくなるので、関係を整理したり数直線に表すことがより重要になってくると思います。
ご意見頂けたら幸いです。
その2に続く!



