共通部分はどこなのかを考えるために
問題です。
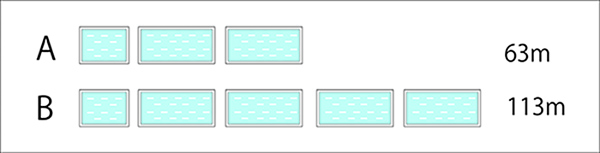
小プールと大プールがあります。
A…小プールは1回、大プールは2回泳いで63m。
B…小プールは1回、大プールは4回泳いで113m。
それぞれ何m?
まずは、図を用いてみます。
先生「Aは、小プール1回と大プール2回で…」
子ども「63m」
先生「Bは、小プール1回と大プール4回で…」
子ども「113m」
先生「今回は共通部分に注目して考えいきます。共通部分を見つけてみましょう」
と、漠然と投げかけてわかる子も少なそうなので、
先生「二人とも…」
といって、次のカードを提示します。↓
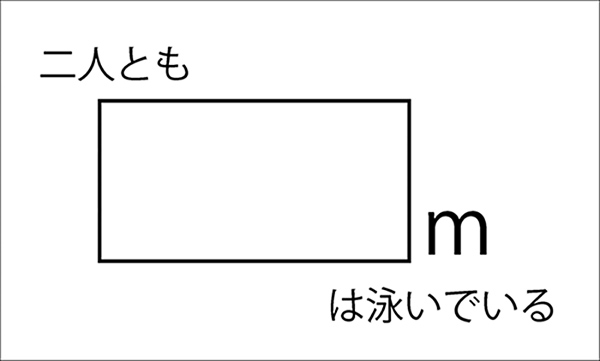
先生「この中には何が入るかな?」
子ども「63m!」
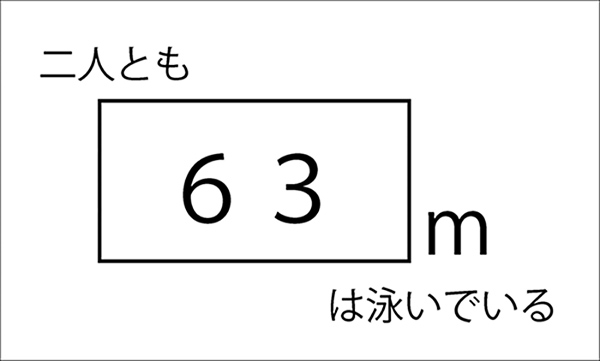
先生「そう、二人とも63mは泳いでいるよね。これが共通部分。どこからどこまでを63mにしょうか?」
といって、前にでて線を引いてもらいます。↓
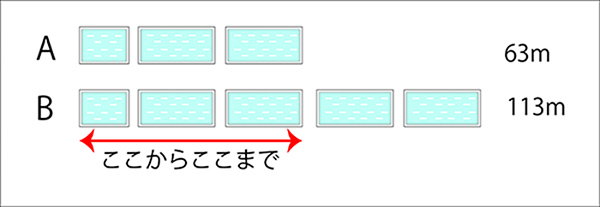
もうわかった子がでてきます。
先生「そうだね。では、ここからそれぞれのプールの長さを考えてもらいますが、図を書きましょう。」↓
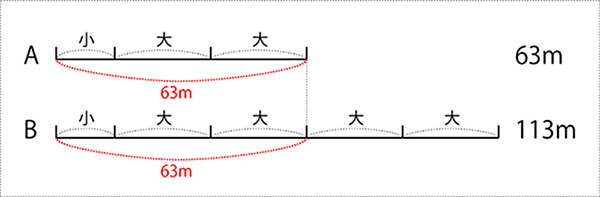
先生「他にどこの長さがわかる?」
子ども「大プール2つ分の長さ!」
先生「なるほど!何メートル?」
子ども「113ー63で50m!」
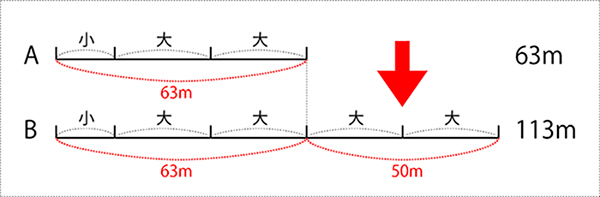
先生「ここまで来れば、もう求められるね!」
と、お膳立てをします。
今回は、少し早く進みましたので、解き方の解説文を書いてもいます。
Aは小プール1回と大プール2回で63メートル。
Bは小プール1回と大プール2回で113メートル。
BからAを引くと50メートルになる。この長さは…
と、ここまで提示しておいて、続きを書いてもらうことにします。
簡単ですがこれは練習用にし、もう一つあある問題では全文書いてもらうことにします。
何事も書き方のフォーマットと知ることは必要です。
フォーマットをたくさん提示することで、形を覚えていきます。
続きは、以下のようにかいてもらえればいいなと思っています。
これは、大プール2回分の長さです。
なので、大プール1回分は50÷2で25m。
小プールは63ー50で13mになる。
解説文はロイロノートで送ると便利ですね!
提出箱に送っていいものを共有するとより深まります!
問題数が少ない分、共通部分をみつけることや図を用いて考えること、解説することなどふだんではじっくりできないような内容を盛り込んでいきます。
4年生最終の単元ということで、そういった力がついたかどうかも確認できますね!
こんかいつかったプールの画像を添付しておきます。
よかったらご利用ください。
ご意見いただければ幸いです。