公式が半径×半径×3.14の理由
この公式を何のヒントもなく、見つけられる小学生がいるのでしょうか!?
ヒントとなるスライドを作って、指導してみました!
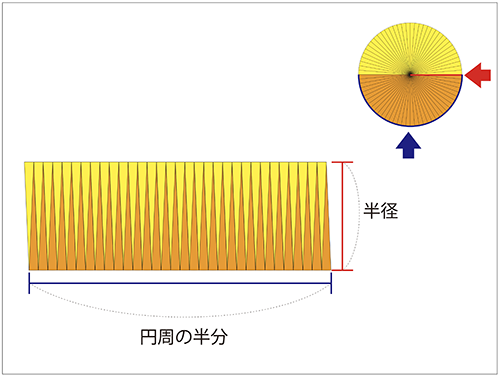
スライドを使った実践例です。
はじめに円の面積は「半径×半径×3.14」と伝え、なぜそうなるかをスライドを使って考えていきました。
↓円を8等分し…
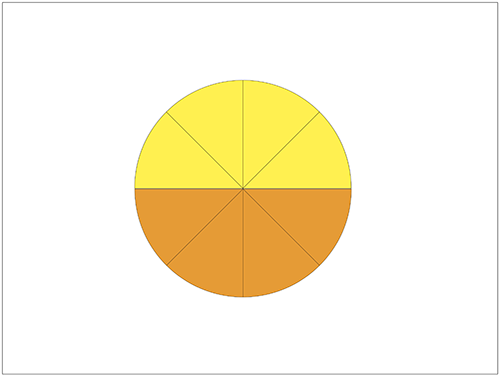
↓形を変えていきます。
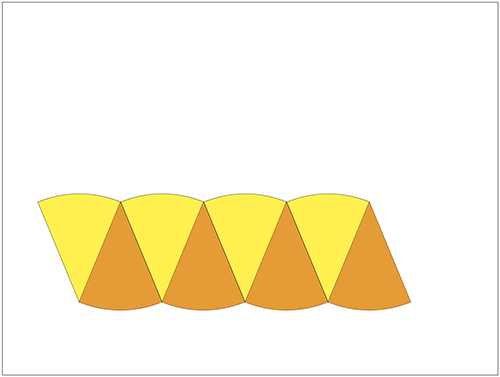
↓もう少し細かく切り分け…
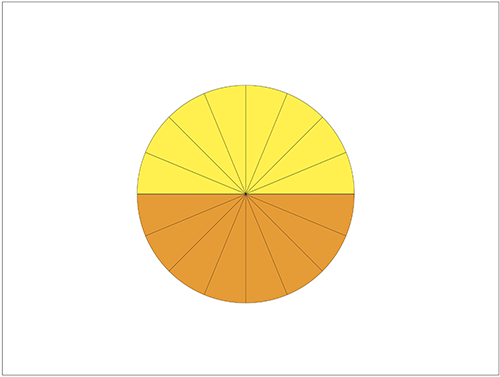
↓形を形を変えてみます。何の形に見えるかな?
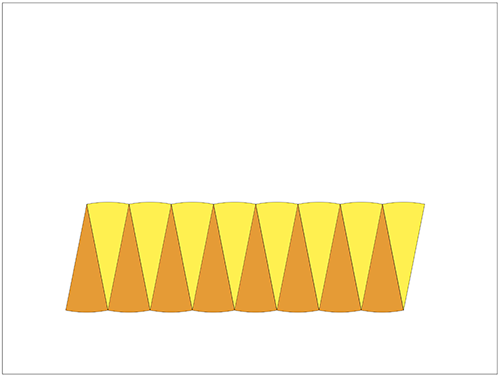
↓さらに細かく…
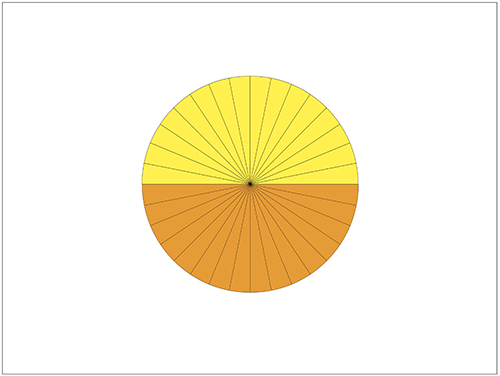
↓ここら辺で子どもたちから「平行四辺形だ!」という声が聞こえてきました。

先生「これよりさらに細かく切り分けるとどうなるかな?」
↓さらに細かく…
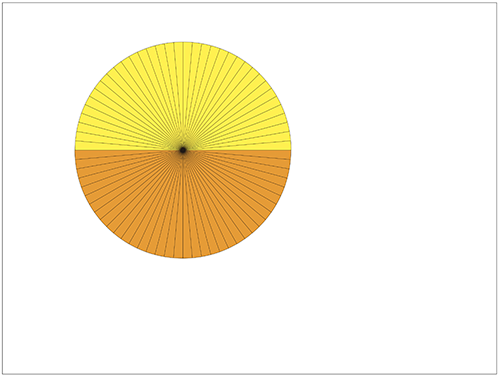
↓子ども「長方形!」

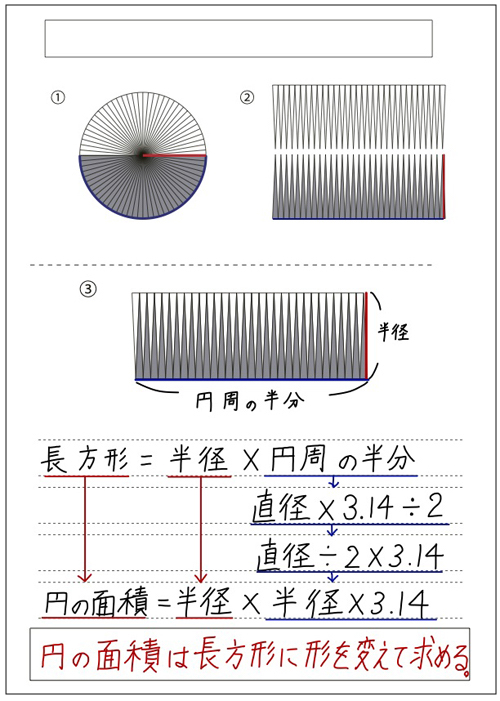
先生「そう!長方形!昔の人は、円を長方形に変えて面積を求めることを考えたんだね!長方形はどのように求めたっけ?」
子ども「たて×横」
↓先生「そうだね!じゃあ、この長方形のたての長さは、円でいうとどこかな?」

↓子ども「半径!」
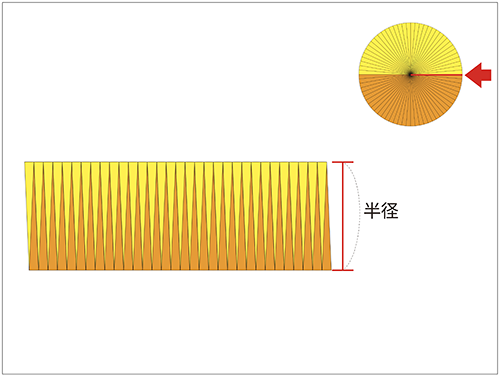
↓先生「じゃぁ、横の長さは?」
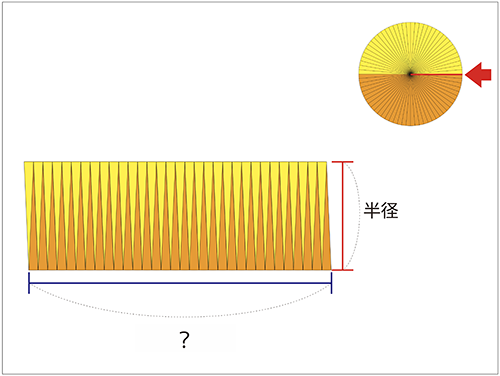
↓子ども「円周の半分!」

先生「そうだね!つまり、円の面積は半径×円周の半分で求められることがわかったね!」
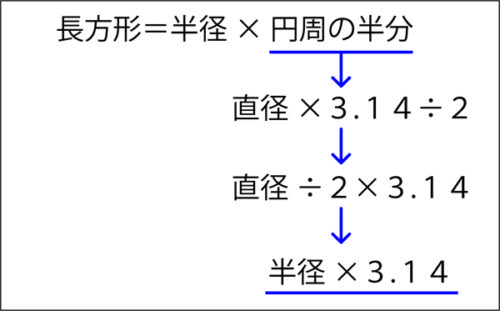
「半径×円周の半分」を「半径×半径×3.14」の形に変える。
↓先生「長方形に形を変えた円は、半径×円周の半分で求められることがわかりました。でも、円の面積は半径×半径×3.14だったよね。円周の半分は、どのように求めますか?」

子ども「直径×3.14÷2」
↓先生「そうだね!」

↓先生「少し計算の順番を変えてみます。直径を先に÷2してみると、直径は何になるかな?」

子ども「半径!」
↓先生「そうだね!つまり、直径×3.14÷2は、半径×3.14という言い方もできるよね。」
ここらへんで子どもたちの中にもわかってきた子が出てきました。
↓先生「そして、はじめの半径をそのまま下ろすと…。」
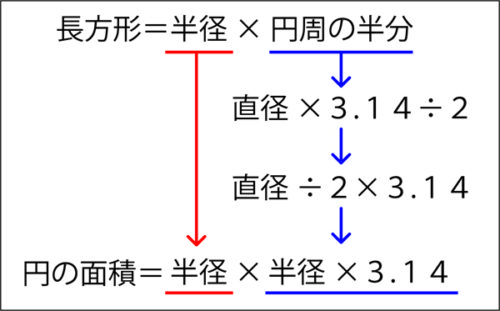
先生「円の面積は、半径×半径×3.14で求めれることがわかりました!」
子ども「おお〜。」
とはいうものの、3日経てば、こんな理由はすぐに忘れられますが…。
「お家の方に、理由を説明しましょう!」といった宿題を出してもいいかもしれませんね(笑)
↓こんなワークシートも作ってみました↓
↓こちらが記入例↓
↓今回紹介したスライド&ワークシートを販売しまします↓