直方体の体積の求め方と同じなので…
角柱の体積を指導するのに、難しいと思わせるのは
「直方体の求め方でいいじゃん」
と、子どもたちに思われてしまう点です。
だから、教師側が説明しても話半分で聞いている子も多いのではと思います。
なので、子どもたちには、
「直方体の求め方でも十分求められるけど、今日学ぶ求め方も知っておくと、今後の体積の求め方の幅が広がります。」
と、あらかじめ断って進めていきました。
では、指導実践です。
まずは直方体の振り返り
まずは、これまで学習した直方体の体積の求め方の復習をします。
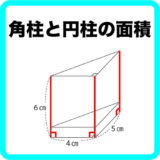
先生「この直方体の求め方は?」
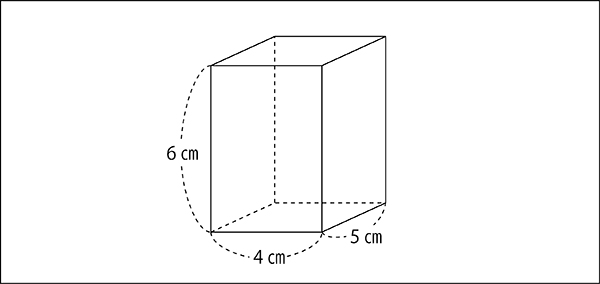
子ども「5×4×6で120㎤」
先生「正解!直方体は、1㎤の立方体が何個分として考えてるんだったね。」
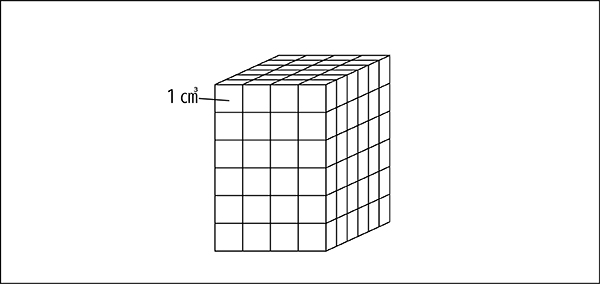
子どもたちはそんなこと忘れていますが…。
先生「縦に5個分、横に4個分、高さに6個分。だから、5×4×6で1㎤の立方体が120個分というところから求めるんだったね。」
そういえばそうだったみたいなリアクションが返ってきます…。
角柱も振り返る
先生「今日は角柱の体積の求め方だけど、その前に角柱を振り返ってみよう。」
底面や側面など名称を振り返ります。
先生「底面から縦にのびる直線は、どのようにのびていますか?」
子ども「垂直」
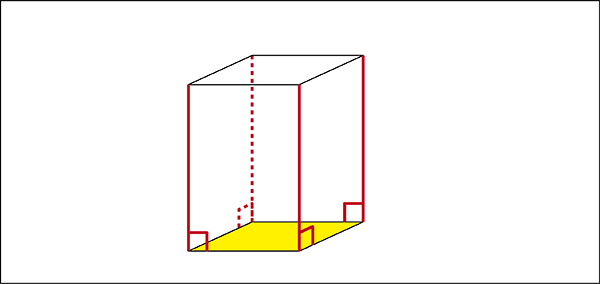
先生「そして、垂直に伸びても底面の形は…。」
子ども「変わらない」
この垂直が角柱の体積の求め方のポイントです。
今後の三角柱や円柱の求め方にも活かすことができます。
角柱の体積の求め方を伝える
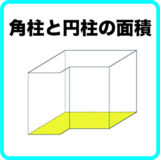
先生「さて、角柱の体積を求めますが、まずは底面の面積を求めます。底面の面積は何㎠?」
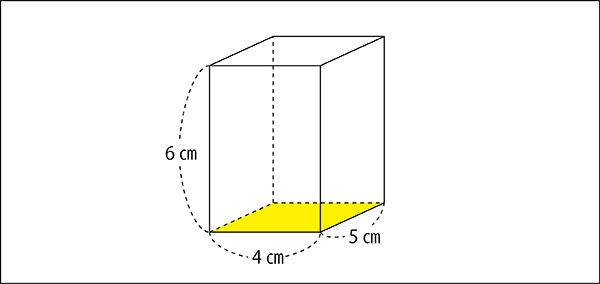
子ども「20㎠。」
先生「その面積に1㎤の立方体が何個積み上がるかを考えていきます。まずは底面に何個しきつめられる?」
子ども「20個。」
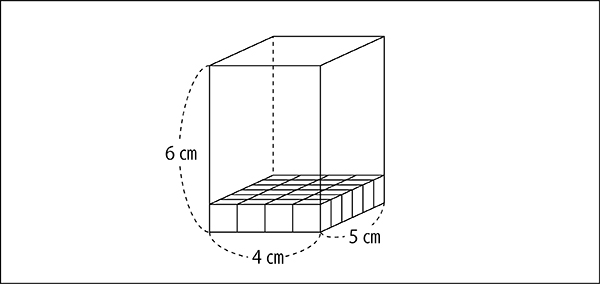
先生「そうだね。だって、底面の面積は20㎠だもんね。面積の大きさと同じ個数の立方体をしきつめられるね。」
先生「角柱は底面から垂直にのびた形だったね。だからこの形のまま縦につみあげられるね。この20㎤の体積は何段積める?」
子ども「6段」
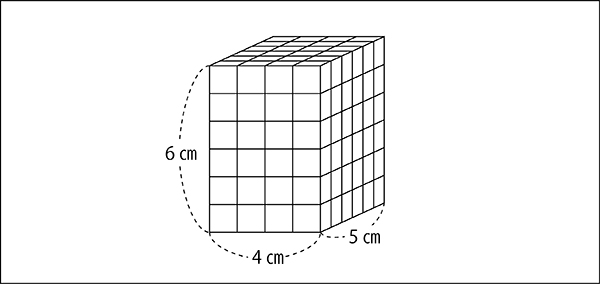
先生「そう。つまり、角柱は底面と同じ形の体積を何段つめるかで求めます。」
公式にする。
先生「底面の面積は20㎠。」

先生「その上に1㎤の体積を敷き詰めていきました。1段目には底面の面積と同じ分しきつめられます。」

先生「そして、角柱は底面から垂直にのびる形なので、そのまま6段つみあげる。」

公式を伝えます。
先生「角柱は底面の面積に1㎤の立方体をしきつめた体積を何段分つむかで求めるので、底面積×高さで求めます。」
練習問題で垂直につみあげることを印象付ける。
先生「では、この問題はどのように求めますか?」
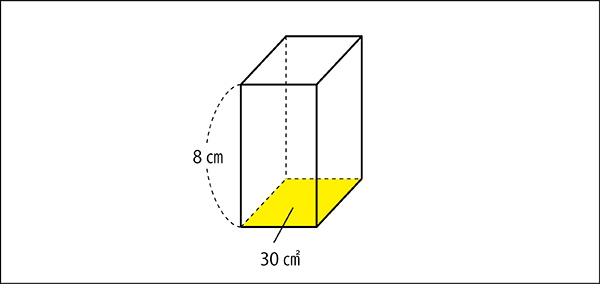
子ども「30×8」
先生「底面積に1㎤の直方体をどれだけしきつめられますか?」
子ども「30個」
先生「その30個をどのように何段つみあげますか。」
子ども「垂直に8段」
先生「だから8をかけるんだね。」
このあと、類似問題をいくつか出題します。
角柱は底面の形にしきつめた立方体をつみあげていくことをおさえて終了しました。
これがおさえられれば、このあとの角柱、円柱がスムーズに進められます。
資料はこちらから!
紹介した画像の資料です。
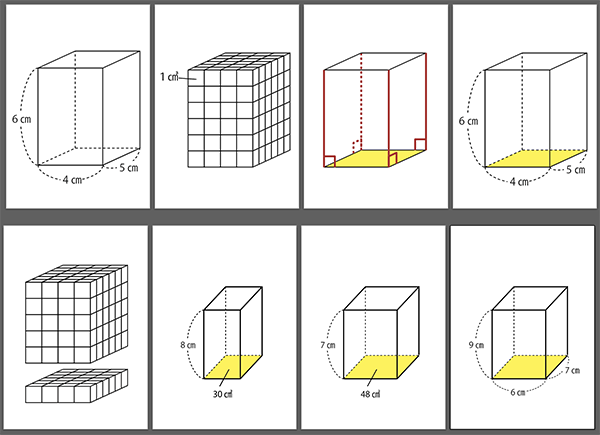
拡大して黒板に掲示できます。
こちらからどうぞ!
ご意見頂けたら幸いです。
↓角柱の体積のその他の記事はこちら↓