いよいよ2けた÷1けた!
第1時の「何十のわり算」で10の束を作ると計算しやすいことをおさえました。
第2時は「何百のわり算」なので、これも10の束のように100の束を作ればよいので、理解は早かったです。
さぁ、いよいよ「72÷3」です。
筆算で解く前の大切な授業です。これまでの授業で、大きい数は束にすることが定着できていれば、問題なく進むと思います!
この授業では、
「2けた÷1けたのわり算を、10の束から計算することを知り、図で表すことができる。」
を目標としました。
それでは実践報告です。
画用紙で作った少し大きめの72枚の折り紙を見せて、
先生「今日もたくさんの折り紙を分けます。分けるコツは何だったかな。」
児童「10の束や100の束にします。」
先生「では今回も束を作っていきますね。」
10の束を作っていくと、7束とバラが2枚になりました。
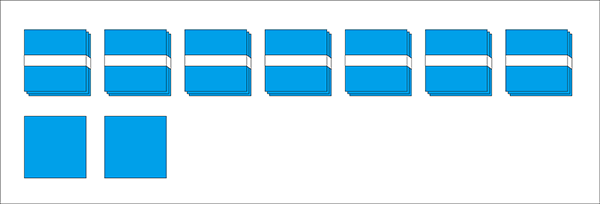
先生「この7束と2枚、合計72枚を3人で分けます。式は?」
児童「72÷3」
先生「どう分けていこうか。束から?それともバラから?」
児童「束になったものから。」
先生「何で?」
児童「バラは2枚しかないから、1人に渡すことができません。」
わり算の筆算の導入で、この72÷3という式は、ほんとによくできてるなと思います。7束は2束ずつ分けられますが、2枚は3人で分けられない。必然的に10の束から分けないといけない状況を作っているわけです。
筆算も十の位から考えます。なので、この考えが非常に重要です。
先生「だよね。最初にどかっともらう方がいいよね。何束ずつ渡せる?」
児童「2束ずつ。」
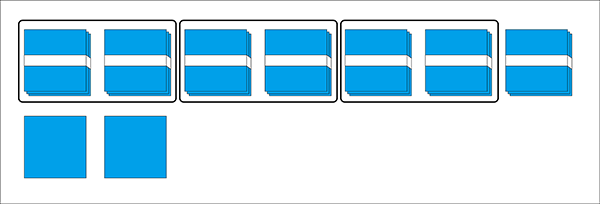
先生「1束と2枚残っちゃった。どうしようか。」

児童「束をばらして、2枚と合わせて12枚にしてから分けます。そうすると、1人4枚ずつ分けられます。」

先生「じゃあ72÷3の答えはどうなるかな?」
児童「24です。」
先生「じゃあ、今のをノートに図をかきながら振り返っていきたいと思います。」
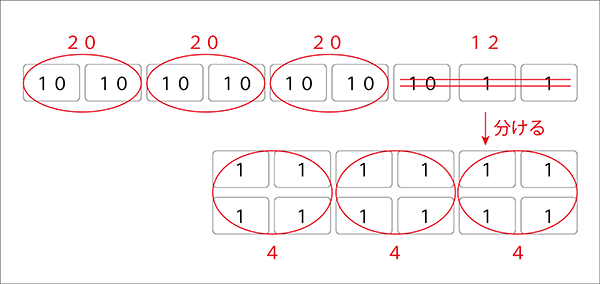
一連の流れを振り返りながらノートにかいて確認します。
この後、類似問題を図で確認しながら解いていきます。まだ筆算には触れません。図をかいて分けることを繰り返して定着を図ります。
類似問題は81÷3や、92÷4などがオススメです。わられる数の一の位が、わる数より小さくないといけません。10の束から分けていきたいからです。
まとめ
10の束から分けていくことがわかれば、十の位から計算する筆算の指導が子どもたちにとってわかりやすくなるのでは思います。
ご意見頂けたら幸いです。
今回使った色紙の資料はこちら
↓4年生のわり算の記事はこちら!↓