第3時は復習の時間にしました。
第3時は、第2時でやった内容を確認と、計算問題をしました。
計算ドリルの問題をしました。
ノートの書き方などもチェックしながら進めていきました。
第4時は、何個ずつ分けると行った包含除の問題です。
第1・2時でやった何人ずつで分ける等分除との違いを印象付けたいですが、詳しくは第5時で取り扱うことにします。
第4時の実践報告です。
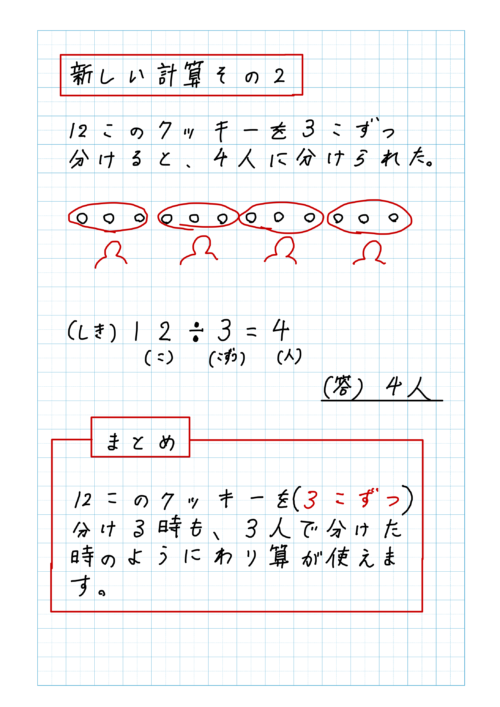
「12個のクッキーを3つずつ分けると4人に分けられる。」を理解する。
先生
「今日も新しい計算の仕方を勉強します。」
12個のクッキーが入った袋を用意します。
先生「この袋の中のクッキーを3つずつ分けていきます。何人に分けられるかな?」

袋の中に何つ入っているかは言いません。
先生「3つずつ分けるから、どうやって渡していけばいい?」
子ども「3ついっぺんに渡せばいい。」
先生「では、3つずつ渡していきます。さあ、何人分あるかな?渡していくので、みんなは数えてくださいね。」
と言って順番に3つずつ子どもたちに渡していきます。
そして、4人目で12個のクッキーが渡し終えました。

先生「何個あったクッキーを何個ずつ分けたら何人に分けられた?」
大事な文です。
子ども「12個あったクッキーを3つずつ分けると、4人に分けられた。」

ノートに書きます。
先生「今までやってきた分け方と違うところあるかな?」
勘の鋭い子、ノートを振り返る子、様々です。
先生「となり同士で話をしてごらん。」
と言って、時間をとり、発表してもらいます。
子ども「今までは3人で分けていたけど、今回のは3つずつ分けた。」
先生「そうですね。今までは、分ける人数が決まっていたけど、今回は分けるものの数が決まっているんだね。」
先生「今回のこの『12個あったクッキーを3つずつ分けたら4人に分けられた』ことも、わり算の式に置き換えることができます。」
と言って、「12(こ)÷3(つずつ)=4(人)」と書きました。
まとめでは、
「12このクッキーを( )分ける時も、3人で分けた時のようにわり算が使えます。」
にして、( )の中を考えさせました。
もちろん、答えは3つずつです。
類似問題で定着させる。
「8こを2こずつ分ける」
「10こを5こずつ分ける。」
などの問題を、文章・図・式・答えのワンセットで書かせました。
第4時のノート計画です。

ご意見いただければ幸いです。
その他の時間のわり算実践報告は、こちらをどうぞ↓
https://kuronekoneko.com/3nenwarizan5/


