できるだけシンプルに。
倍数を学んだあとの約数です。
導入をあまり複雑にすると、子どもたちも頭が混乱してしまうおそれがあります。
なので、第1時は、シンプルにその数をわることだけに特化して進めていきました。
では、指導実践です。
↓先生「12このあめを、ある人数で分けます。何人でわけられる?」

子ども「2人」
↓図のあめを分けていきます。

また、新しい図を黒板に貼ります。
先生「他にもある?」
子ども「3人」

子ども「6人」

など、答えてもらいます。
「1人!」
と答えたあとは、
「1人で12こ全部もらえるね〜!」
と、盛り上がりました。
まとめる
全部でたところで、まとめていきます。
先生「分けられる人数は、これで全部だね。」
↓答えてもらった図を数の小さい順にならべていきます。
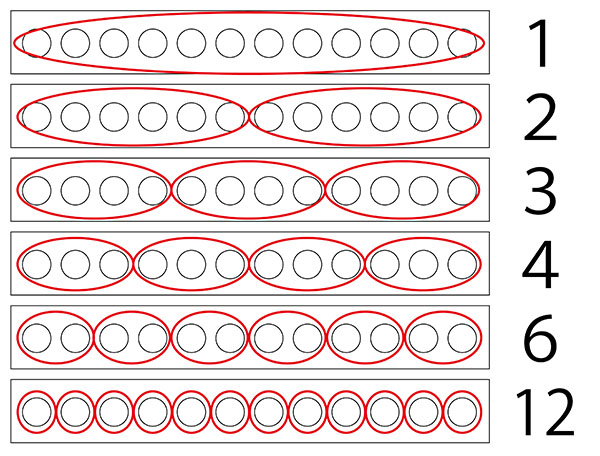
先生「12は、1・2・3・4・6・12の数でわることができました。この数を12の約数といいます。」
これで終了です。
ここまででおよそ15分くらいでしょうか。
残りはたっぷりと練習問題の時間にあてます。
練習問題をしながら、約数の特徴を見つける。
先生「練習問題1問目は18。われる数字をさがしてごらん。」
まずは、バラバラでもいいので、書き出させます。
そして、確認していきます。
答えの数字をいい、書き出しものに◯をつけていきます。
そのあとも、16や9、15などの簡単な問題を中心に練習していきます。
いくつかやっていく間に、質問を投げかけます。
先生「絶対にある約数って何?」
子ども「1!」
とか、
先生「偶数だったら何でわれる?」
子ども「2!」
とか、
先生「18だったら、絶対にある約数は?」
子ども「18!」
など、問題をこなしながら特徴をつかんでいきます。
問題で、7などの素数をだすと、約数が2つしかなので混乱する子もいますが、
先生「2つしかない場合もあるんだね。」
といって、11や17などの数も続けて出題してみます。
第1時の授業はここまで!
練習問題をしているときの注意
やみくもに約数を書き出していると、一体これは何の作業だろうとわからなくなってしまうこともあります。
なので、
先生「今、書き出しているのは何?」
先生「書き出したその数は、9の何?」
など、今やっている作業がなんなのかということを理解させながら進めていきました。
ご意見頂けたら幸いです。