実践報告です。
第2時では、あまりあるわり算をくわしく知っていく時間にしたいと思います。
第2時で行うことは、
・「わりきれる」「わりきれない」を知る。
・あまりあるわり算も九九を用いて答えを出すことができることを知る。
です!
「わりきれる」「わりきれない」を知る。
先生「今回のわり算ように、あまりがでる場合は『わりきれない』といいます。あまりがでない場合は、『わりきれる』といいます。」
いくつかスライドで確かめていきます。
先生「次の式は、わりきれる?わりきれない?」
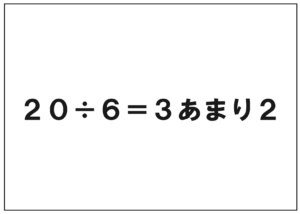
子ども「わりきれない」
先生「何で?」
子ども「あまりがあるから。」
理由も確認していきます。
このあと、いくつか立て続けにスライドを見せていきます。
先生「次の式は?」
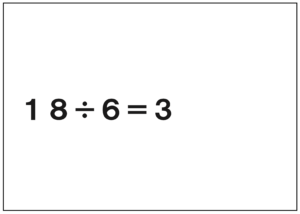
子ども「わりきれる!」
先生「何で?」
子ども「あまりがないから。」
といった具合に、テンポよく確認しました。
あまりあるわり算も九九を用いて答えを出すことができることを知る
先生「じゃあこの式はどっち?」
答えを書いてないスライドを出します。
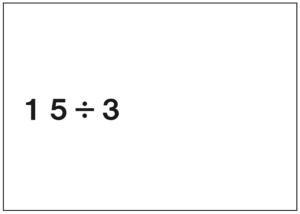
子ども「わりきれる。」
先生「これは?」
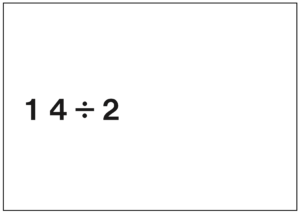
子ども「これもわりきれる。」
先生「これは?」
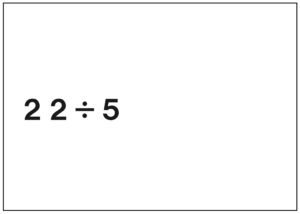
子ども「え?あ?うーん、わりきれない。」
子ども「わりきれる!」
迷い始める子がでてきます。
続けます。
先生「これは?」
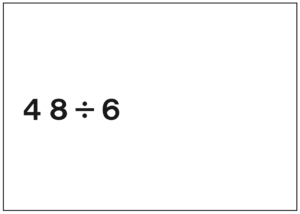
子ども「わりきれる。」
先生「これは?」
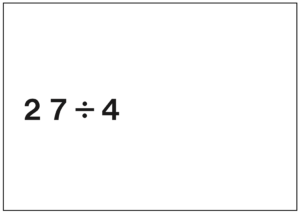
子ども「わりきれない!」
子ども「えーっと…」
先生「今、『わりきれる』『わりきれない』を早く気づくことができた人?」
パラパラ手が挙がります。
先生「どうやったら早く見つけることができるの?最後に出てきた27÷4はわりきれないって言ってたけど。」
となり同士で話し合ってもらいます。(ペアトーク)
子ども「わりきれないやつは、答えが九九の中にない。」
先生「どういうこと?」
子ども「たとえば、15÷3は、3の段の九九で見つけることができるけど、27÷4は、4の段の九九で答えをさがしても27はない。」
先生「なるほど。」
スライドの問題を確認していきます。
先生「じゃあ、わりきれないわり算は、どうやって答えをだせばいいんだろう?今までみたいに、毎回図をかくのは大変だよ。」
子ども「わりきれない時も九九を使える。」
先生「どういう風に使うの?」
子ども「27÷4だったら、27に近い九九を探していく。この場合、6が一番近いから4×6で24になって、27から引いてでた3があまり。」
私も、27個の◯を黒板に書いて説明を補足しました。
先生「なるほど。でも、7はだめなの?4×7で28。27に一番近いけど。」
子ども「28は27を超えるからダメ。」
先生「超えてはダメ?」
子ども「もともとあった数は27だから。」
練習問題に進む。
このあと、いくつか九九を使って練習問題をしました。
1問ずつ、確認しながら進めていきます。
「16÷3」や「17÷2」「27÷5」など、3問程度行いました。
授業を終えて
やはり、説明になると、ちんぷんかんぷんの子も何人かでてきました。
あとで、質問に来る子も何人かいました。
次の時間は、あまりあるわり算の計算問題を解く時間にしました。
ご意見いただければ幸いです。
↓第3時に続く!

3年算数「あまりのあるわり算」第3時 指導実践報告 計算の練習を授業でたっぷりと。

3年算数「あまりのあるわり算」第4時 指導実践報告〈あまりはわる数より小さくなる〉

3年算数「あまりのあるわり算」第5時 指導実践報告〈たしかめの式〉

3年算数「あまりのあるわり算」第6時 指導実践報告〈あまりを考える問題〉


