では、指導実践です。
よくある長方形を並べて正方形をつくる問題です。
↓先生「たて6cm、横8cmの長方形があります。」
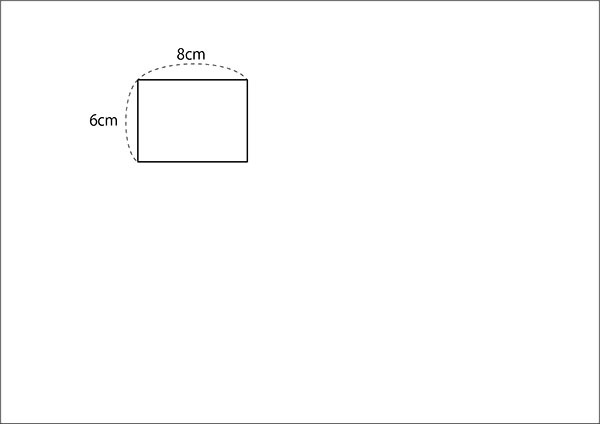
↓先生「こうして、長方形をならべて最小枚数で正方形にしたいんだけど、今はどうかな?」
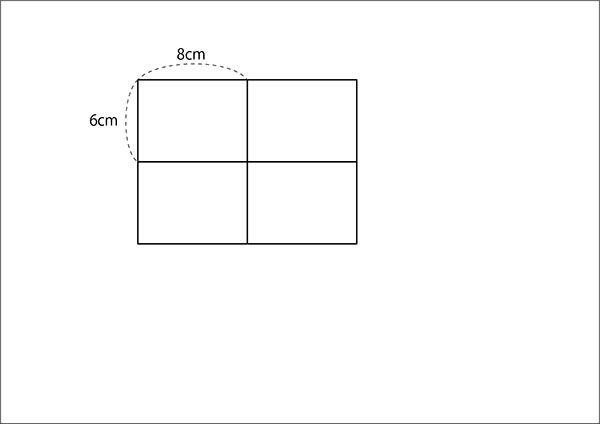
子ども「なってない。」
先生「今は、たて・横それぞれ何cm?」
子ども「たて12cm、横16cm」
先生「う〜ん、もう少し並べてみようか。何cmで正方形になるかなぁ。」
もう、検討がついている子どもが手を挙げます。
子ども「24cm!」
先生「本当〜?じゃぁ、たてにあと何枚並べる?」
子ども「2枚!」
↓先生「2枚並べると、合計4枚だから、6×4で24だね。」
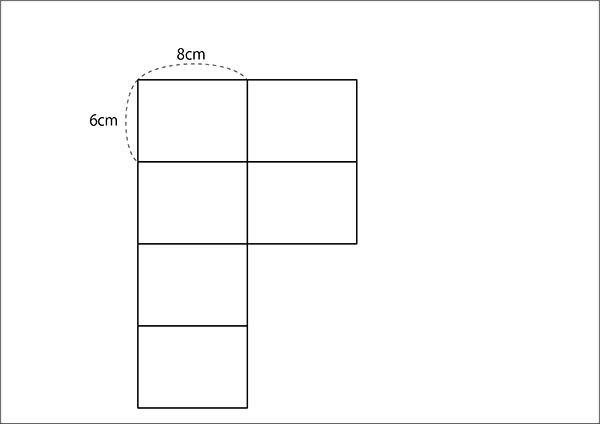
先生「横には?」
子ども「1枚!」
先生「そうすると、どうなる?」
子ども「8×3で24cm」
↓先生「ほんとだ!24cmずつで、正方形になりそうだね!」
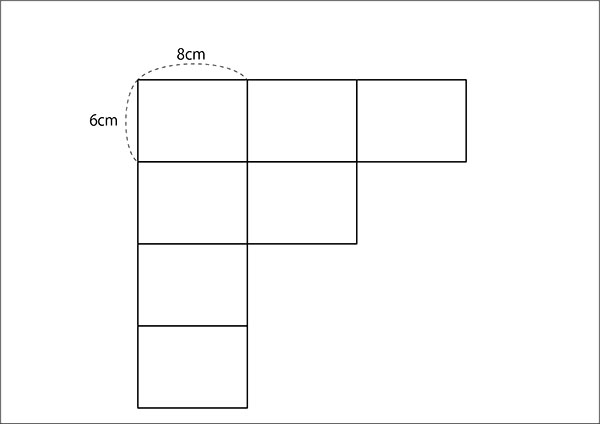
先生「ちなみに長方形が何枚いるの?」
子ども「12枚」
↓先生「実際に並べてみます。」
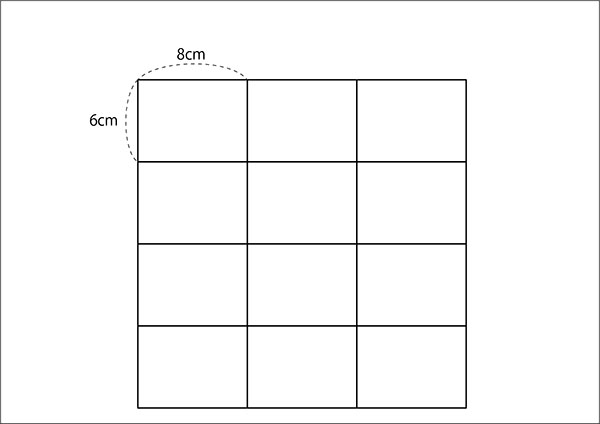
先生「ほんとだ!12枚!」
問題文を考えてみる。
今回は、一連の流れを先に見せて、あとで問題文を考えてみることにしました。
先生「長方形を並べて、正方形をつくり、1辺が何cmで、長方形が何枚いるかを求めて行きました。どんな問題文になりそう?」
ここまで言うと、うまく問題文を作ってくれました。
先生「この問題を解くとき、いつもこうして長方形を使って並べていかないといけないかな?24cmって、結局何なの?」
子ども「最小公倍数!」
ずっと公倍数を練習してきたので、スッと「最小公倍数」と出てくるかと思ったのですが、案外こうして形をかえるとなかなか出てきませんでした。
長方形の枚数も、最小公倍数から求めることを確認して、終了です。

先生「この流れだと、いちいち長方形を使わなくても問題が解けるね!」
練習問題
練習問題は、具体物なしで、問題を解いていきます。
先ほどの流れを用いて解いていきました。
ご意見頂けたら幸いです。