単位量の理解が深まる!
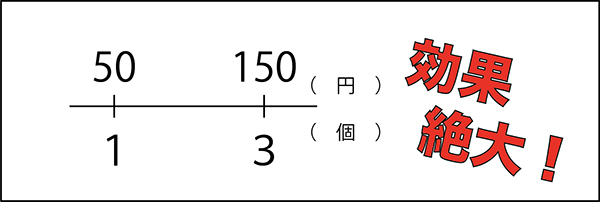
単位量指導の前に、これまで、感覚で使ってきたかけ算・わり算を、改めて数直線を使って確認することをオススメします。
どの学年の教科書にも必ず出てきます。
単位量では、「1㎡あたり」「1匹あたり」など、何でわればよいか混乱することがよくあります。
かけ算・わり算の関係を数直線を使って視覚的に表すことで、その混乱を防ぐことができると思います。
簡単な数字から確認する。
指導のときは、簡単な問題から行いました。
「1個50円の大福があります。3個では何円ですか。」
誰でも式と答えを導き出すことができるはずです。
でも、これをちゃんと数直線で表すことに意味があります。
先生「1個の3倍が3個だから、50円も3倍するんだね。」
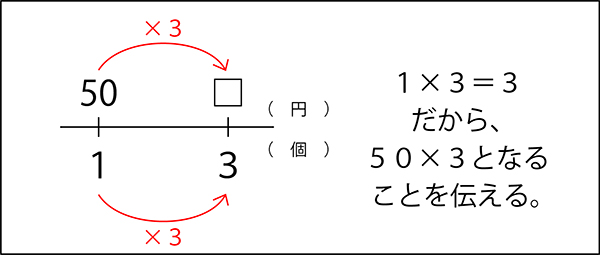
類似問題をいくつかしたら、わり算にします。
「5個で360円のチョコレートがあります。1個何円ですか。」
お金にするのは、子どもたちにわかりやすいからです。
これも、すぐに式が導きだされます。
数直線で考える際、私は、わり算でも1の何倍というところから考えさせます。
その方が、かけ算・わり算のどちらも共通して、1からやじるしを伸ばして考えることができるからです。
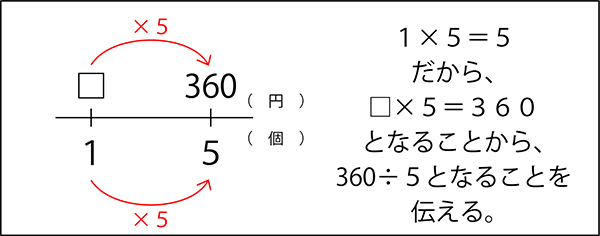
先生「わり算は、□×5=360だから、360÷5になるんだね。」
ここまでがレベル1。
次は、単位量につながる問題を練習します。
どちらが「1」か、考えさせる。
「40枚で200gの紙があります。1枚何gですか。」
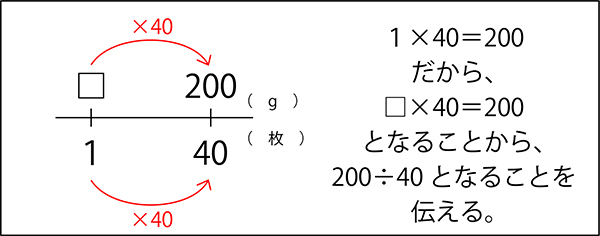
式は「200÷40=5」
答えは「5g」です。
そして、次に、
「40枚で200gの紙があります。1g何枚ですか。」
と問います。
そして、どちらに1を書くか考えさせます。

…とは言っても、簡単に書くことができます。
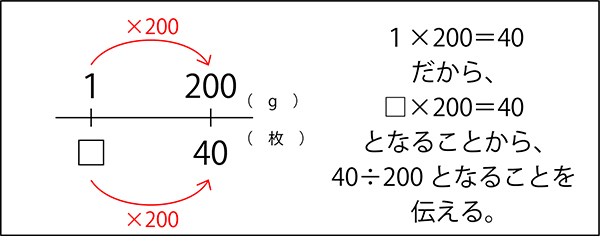
先生「式は、□×200=40。40÷200=0.5 答えは0.2枚だね。」
もう、ここまできたら、ほぼ単位量もできたも同然です。
先生「問われていることで、どちらに1を書くか考えないといけないね。」
しっかり数直線を書く技を身につけて、単位量に進むと、驚くほどスムーズに授業が進みました。
この後の速さも、数直線とともに進めていきます。
ご意見頂けたら幸いです。


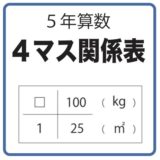


良い教授法だと思いましたが,最後の図について多少ひっかかる部分がありました。紙を0.2枚と数えることは現実世界ではなかなかないかもですね。