公式につながる授業を目指して
子どもたちに自由に面積を求めさせても、結局最後は公式にあてはめます。
なので、今回は、できるだけ公式につながる授業展開を目指して授業を組み立ててみました。
では、指導実践です。
先生「今日は、この台形を求めます。↓」
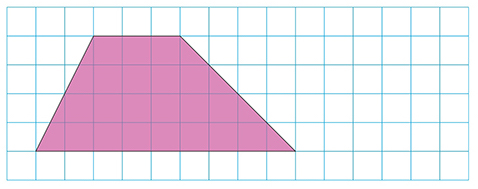
先生「いろいろな求め方があるけれど、今日は2つの台形から求め方を考えてもらいます。」
上のピンクの台形を子どもたちに渡した後、同じ形の台形も渡します。
先生「2つ合わせると、何か見えてこないかな。」
子ども「あ、平行四辺形だ!」
先生「そう。その通り!」
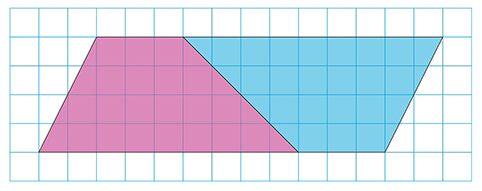
先生「じゃぁ、ここから台形の面積をどうやって求めようか。」
ペアトークさせます。
子ども「台形を2つ合わせて平行四辺形をつくって、その面積を求めてから半分にわる。」
先生「なるほど!何かの求め方に似てない?」
子ども「あ、三角形だ。」
先生「どんなところが似てる?」
子ども「平行四辺形を2でわるところ。」
先生「そうだね。じゃぁ、平行四辺形や三角形の面積を求める公式を思い出しながら解いてごらん。」
少し時間をとった後…。
先生「面積はいくつになった?」
子ども「24㎠。」
先生「どうやって求めましたか?」
子ども「まずは、平行四辺形を求めるから、底辺12㎝と高さの4㎝をかけて48㎠で…。」
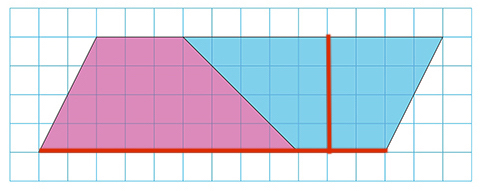
↑図に底辺と高さを加えます。
子ども「それから2でわると、24㎠になります。」
先生「なるほど、じゃあ台形も、三角形と同じように底辺×高さ÷2で求められるね。」
板書します。

先生「でも、三角形の時と比べて、ここは気をつけないといけないってところない?」
ペアトークをさせます。
子ども「台形のときは、上の辺と下の辺が合わさった長さが底辺になる。」

先生「ちなみに、底辺の長さを求めた式は?」
子ども「8+4。」
板書に付け加えていきます。

先生「これが、台形の面積の公式になりそうだね。」
上の辺を上底、下の辺を下底と言うことを教え、公式を伝えます。
繰り返し、公式の意味を確認する。
先生「上底と下底を合わせて何ができるの?」
子ども「底辺。」
先生「その底辺と高さをかけると、どんな図形ができる?」
子ども「平行四辺形。」
先生「その平行四辺形は、台形何個分?」
子ども「2つ分。」
先生「だから最後に…。」
子ども「わる!」
先生「となりの子にも、公式の意味を説明しなさい。」
となり同士で説明する時間をとります。
説明するという、アウトプット活動で定着をはかります。
学んだことをアウトプットする活動を。
その後で、みんなの前で説明したい子を当てて説明させました。
授業を終えて。
台形の公式が、なぜあの形なのかを理解する1時間となりました。
既習の平行四辺形と三角形の面積の公式を使いながらなので、学びのつながりも感じることができました。
また、結構スムーズに進むので、1時間で練習問題にも進むことができました。
ただ、やはり1から面積の求め方を考えたい子もちらほら…。
時間のない時には、今回の授業のようなものでもいいのかもしれません。
ご意見いただけたら幸いです。
今回使った素材は、こちら
↓面積の指導実践はこちら!↓





